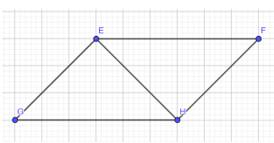
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) \(\Delta EFH=\Delta HGE\)
b) EF // HG
Cho ΔDEF có : DE = DF = 5cm ; EF = 8cm ; Kẻ DH ⊥ EF ( H ∈ EF )
a) Chứng minh : HE = HF ; góc EDH = góc FDH
b) Tính DH
c) Kẻ HK ⊥ DE ( K ∈ DE ) ; Kẻ HG ⊥ DF ( G ∈ DF )
Chứng minh : ΔHKG là tam giác cân
a: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của EF và DH là phân giác của góc EDF
=>góc EDH=góc FDH
b: EH=FH=8/2=4cm
=>DH=3cm
c: Xét ΔDKH vuông tại K và ΔDGH vuông tại G có
DH chung
góc KDH=góc GDH
=>ΔDKH=ΔDGH
=>HK=HG
=>ΔHKG cân tại H
Cho tam giác EFG và điểm H nằm trên cạnh EG. Nối FH.Trên đoạn thẳng FH lấy điểm I bất kỳ.Nối IG a/Chứng minh góc FIG > FEG b/Chứng minh EF + EG > HF + HG
a) Ta có: \(\widehat{FIG}+\widehat{IFG}+\widehat{IGF}=180^0\)( tổng 3 góc trong △FIG)
\(\widehat{FEG}+\widehat{EFG}+\widehat{EGF}=180^0\)( tổng 3 góc trong △FEG)
Mà \(\widehat{IFG}< \widehat{EFG}\left(\widehat{IFG}+\stackrel\frown{EFI}=\widehat{EFG}\right)\)
\(\widehat{IGF}< \widehat{EGF}\left(\widehat{IGF}+\widehat{EGI}=\widehat{EGF}\right)\)
=>\(\widehat{FIG}>\widehat{FEG}\)
b) Ta có: EF + HE>FH (bất đẳng thức trong △EFG)
=>EF+EH+HG>FH+HG
=>EF+EG>FH+HG
Cho hình thang EFHG (EF//HG). Gọi A, B lần lượt là trung điểm của EG và FH.
a) Chứng minh: AB là đường trung bình của hình thang EFHG
b) Cho EF= 5cm, AB=7cm. Tính HG
4.Cho biết △MNP =△DEF và MN = 4 cm,MP= 5 cm ,EF=6 cm . Tính chu vi tam giác MNP.
6. Cho hình 25 có EF= HG,EG =HF.
Chứng minh rằng :
a) △EFH = △HGE.
b)EF // HG.
8.Cho góc xOy. Lấy hai điểm A,B thuộc tia Ox sao cho OA < OB .Lấy hai điểm C,D thuộc tia Oy sao cho OC = OA ,OD = OB .Gọi E là giao điểm của AD và BC .Chứng minh rằng:
a) AD = BC.
b) △EAB = △ECD.
c) OE là tia phân giác của góc xOy.
-giúp bài này với mình cần gấp trong hôm nay.
Cho Δ DEF vuông tại D, trên cạnh EF lấy điểm N sao cho EN=ED. Qua N vẽ đường vuông góc EF tại N cắt DF tại O.
a) Chứng minh: Δ EOD= Δ EON
b) Trên tia đối của tia DE lấy điểm H sao cho DE=DH. Chứng minh: Δ EFH cân
c) Trên tia HF lấy điểm M sao cho HM=EN. Chứng minh: MN// EH.
Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)

Chứng minh rằng:
a) \(\Delta EID = \Delta EIF\)
b) Tam giác DIF cân
a) Do EI là tia phân giác của \(\widehat{DEF}\Rightarrow\widehat{DEF}=\widehat{FEI}\)
Xét \(\Delta EID\) và \(\Delta EIF\) có:
ED = EF (theo giả thiết)
\(\widehat{DEI}=\widehat{FEI}\) (chứng minh trên)
EI chung
\(\Rightarrow\Delta EID=\Delta EIF\left(c.g.c\right)\)
b) Do \(\Delta EID=\Delta EIF\Rightarrow ID=IF\) (2 cạnh tương ứng)
\(\Rightarrow\Delta DIF\) cân tại I
Cho hình thang EFGH(EF//GH) có HEF=HEF và EF=9cm, GH=16cm. a) Chứng minh rằng ∆EFH đồng dạng với ∆FHG b) Chứng minh: HF=EF.HG và tính độ dài cạnh HF
Sửa đề: góc E=góc HFG
a: Xét ΔEFH và ΔFHG có
góc EFH=góc FHG
góc E=góc HFG
=>ΔEFH đồng dạng với ΔFHG
b: ΔEFH đồng dạng với ΔFHG
=>HF/HG=EF/HF
=>HF^2=HG*EF=9*16=144
=>FH=12cm
Cho tam giác DEF có M là trung điểm của EF. Trên tia đối của tia MD lấy điểm I sao cho MI=MD.
a) Chứng minh DE=IF, DE//IF.
b) Vẽ DH vuông góc với EF ( H thuộc EF), trên tia đối của tia HD lấy điểm G sao cho HG=HD. Chứng minh EG=IF.
Vì M là trung điểm của EF => ME = MF
Xét △MDE và △MIF
Có : ME = MF (gt)
DME = FMI (2 góc đối đỉnh)
MD = MI (gt)
=> △MDE = △MIF (c.g.c)
=> DE = IF (2 cạnh tương ứng)
Và DEM = MFI (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> DE // IF (dhnb)
b, Vì △MDE = △MIF (cmt)
=> DE = IF (2 cạnh tương ứng)
Xét △HDE vuông tại H và △HGE vuông tại H
Có: HD = HG (gt)
HE : cạnh chung
=> △HDE = △HGE (cgv)
=> DE = GE (2 cạnh tương ứng)
Mà DE = IF (cmt)
=> EG = IF (đpcm)
Cho tam giác EFG, có EG=z ; EF=6. Kẻ EH vuông góc với FG để HG=9 ; HF =x. Gọi EH=y.Tính x,y,z.