Tính (x3 – 2x2 + x – 1)(3x – 2). Trình bày lời giải theo 2 cách.
QL
Những câu hỏi liên quan
Giải các phương trình sau:a)
1
−
2
x
2
3
x
x
−
3
+
x
−
1
2
;
b)
1
+
x...
Đọc tiếp
Giải các phương trình sau:
a) 1 − 2 x 2 = 3 x x − 3 + x − 1 2 ;
b) 1 + x 3 + 1 − x 3 = 6 x + 1 2 ;
c) x − 4 4 − x + 3 = x 3 − 2 − x 6 ;
d) 5 x + 3 x − 4 5 15 = 3 − x 15 + 7 x 5 + 1 − x .
a) x = 0 b) x = - 1 3
c) x = 28 15 d) x = -82.
Đúng 0
Bình luận (0)
Giải phương trình :
1) √x2+x+2 + 1/x= 13-7x/2
2) x2 + 3x = √1-x + 1/4
3) ( x+3)√48-x2-8x= 28-x/ x+3
4) √-x2-2x +48= 28-x/x+3
5) 3x2 + 2(x-1)√2x2-3x +1= 5x + 2
6) 4x2 +(8x - 4)√x -1 = 3x+2√2x2 +5x-3
7) x3/ √16-x2 + x2 -16 = 0
Cho hai đa thức
P
(
x
)
2
x
3
-
3
x
+
x
5
-
4
x
3
+
4
x
-
x
5
+
x
2
-
2
;
Q
(
x
)...
Đọc tiếp
Cho hai đa thức
P ( x ) = 2 x 3 - 3 x + x 5 - 4 x 3 + 4 x - x 5 + x 2 - 2 ; Q ( x ) = x 3 - 2 x 2 + 3 x + 1 + 2 x 2
Tính P(x) - Q(x)
A. - 3 x 3 + x 2 - 2 x + 1
B. - 3 x 3 + x 2 - 2 x - 3
C. 3 x 3 + x 2 - 2 x - 3
D. - x 3 + x 2 - 2 x - 3
Ta có
P ( x ) = 2 x 3 − 3 x + x 5 − 4 x 3 + 4 x − x 5 + x 2 − 2 = x 5 − x 5 + 2 x 3 − 4 x 3 + x 2 + ( 4 x − 3 x ) − 2 = − 2 x 3 + x 2 + x − 2 Và Q ( x ) = x 3 − 2 x 2 + 3 x + 1 + 2 x 2
= x 3 + - 2 x 2 + 2 x 2 + 3 x + 1 = x 3 + 3 x + 1
Khi đó
P ( x ) − Q ( x ) = − 2 x 3 + x 2 + x − 2 − x 3 + 3 x + 1 = − 2 x 3 + x 2 + x − 2 − x 3 − 3 x − 1 = − 2 x 3 − x 3 + x 2 + ( x − 3 x ) − 2 − 1 = − 3 x 3 + x 2 − 2 x − 3
Chọn đáp án B
Đúng 0
Bình luận (0)
Bài 2. Cho các đa thức: f(x) x3 - 2x2 + 3x + 1; g(x) x3 + x - 1; h(x) 2x2 - 1a) Tính f (x) - g(x) + h(x).b) Tìm x sao cho f (x) - g(x) + h(x) 0.Bài 3. Cho các đa thức: f (x) x3 - 2x + 1; g(x) 2x2 - x3 + x - 3a) Tính f (x) + g(x);f(x) - g(x).b) Tính f (x) + g(x) tại x -1; x -2.Bài 4. Cho đa thức: A -2xy2 + 3xy + 5xy2 + 5xy + 1.a) Thu gọn và tìm bậc của đa thức A.b) Tính giá trị của A tại x 12 ; y -1.
Đọc tiếp
Bài 2. Cho các đa thức: f(x) = x3 - 2x2 + 3x + 1; g(x) = x3 + x - 1; h(x) = 2x2 - 1
a) Tính f (x) - g(x) + h(x).
b) Tìm x sao cho f (x) - g(x) + h(x) = 0.
Bài 3. Cho các đa thức: f (x) = x3 - 2x + 1; g(x) = 2x2 - x3 + x - 3
a) Tính f (x) + g(x);f(x) - g(x).
b) Tính f (x) + g(x) tại x = -1; x = -2.
Bài 4. Cho đa thức: A = -2xy2 + 3xy + 5xy2 + 5xy + 1.
a) Thu gọn và tìm bậc của đa thức A.
b) Tính giá trị của A tại x = 1
2
; y = -1.
câu 4: b, đề bài là tính giá trị của A tại x =-1/2;y=-1
Đúng 0
Bình luận (0)
Tk
Bài 2
a) F(x)-G(x)+H(x)= \(x^3-2x^2+3x+1-\left(x^3+x-1\right)+\left(2x^2-1\right)\)
= \(x^3-2x^2+3x+1-x^3-x+1+2x^2-1\)
= \(x^3-x^3-2x^2+2x^2+3x-x+1+1-1\)
= 2x + 1
b) 2x + 1 = 0
2x = -1
x=\(\dfrac{-1}{2}\)
Đúng 2
Bình luận (1)
Tk
Bài 3
a)
f(x) + g(x)
\(x^3-2x+1+\left(2x^2-x^3+x-3\right)\)
\(x^3-2x+1+2x^2-x^3+x-3\)
\(x^3-x^3-2x+x+1-3+2x^2\)
\(-x-2+2x^2\)
f(x) - g(x)
\(x^3-2x+1-\left(2x^2-x^3+x-3\right)\)
\(x^3-2x+1-2x^2+x^3-x+3\)
\(x^3+x^3-2x-x+1+3-2x^2\)
\(2x^3-3x+4-2x^2\)
b)
Thay x = -1, ta có:
\(-\left(-1\right)-2+2\left(-1\right)^2\) = 1
x = -2, ta có
\(2\left(-2\right)^3-3\left(-2\right)+4-2\left(-2\right)^2\)
\(2\cdot\left(-8\right)+6+4-8\) = -14
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bài 1 : giải phương trình
a) (8x + 3)(2x - 1) = (2x - 1)2
b) (x - 5)2 - 36 = 0
c) (4x - 3)2 - 4(x + 3)2
d) x3 - 3x -2 = 0
e) x3 + 2x2 - 4x - 8 = 0
Giải các phương trình sau:
a, x2 - 9x +20 = 0
b, x2 - 3x - 18 = 0
c, 2x2 - 9 x + 9 = 0
d, 3x2 - 8x + 4 = 0
e, 3x3 - 6x2 - 9x = 0
f, x(x - 5) - 2 + x = 0
g, x3 + 32 + 6x +8 = 0
h, 2x(x - 2) - 2 + x = 0
i, 5x(1 - x) + x - 1 = 0
k, 4 - 9(x - 1)2 = 0
l, (x - 2)2 - 36(x + 3)2 = 0
\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
d: \(\Leftrightarrow3x^2-6x-2x+4=0\)
=>(x-2)(3x-2)=0
=>x=2 hoặc x=2/3
e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)
=>x(x-3)(x+1)=0
hay \(x\in\left\{0;3;-1\right\}\)
f: \(\Leftrightarrow x^2-5x-2+x=0\)
\(\Leftrightarrow x^2-4x-2=0\)
\(\Leftrightarrow\left(x-2\right)^2=6\)
hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)
Đúng 0
Bình luận (0)
Bài 2: Cho hai đa thức f(x) 3x + x3 + 2x2 + 4 g(x) x3 + 3x + 1 – x2a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến. b) Tính f(x) + g(x) và f(x) – g(x)c) Chứng tỏ f(x) – g(x) không có nghiệm ai giúp mk với :)) mk cảm ơn !
Đọc tiếp
Bài 2: Cho hai đa thức
f(x) = 3x + x3 + 2x2 + 4
g(x) = x3 + 3x + 1 – x2
a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến. ![]()
b) Tính f(x) + g(x) và f(x) – g(x)
c) Chứng tỏ f(x) – g(x) không có nghiệm
ai giúp mk với :)) mk cảm ơn !
a: \(F\left(x\right)=x^3+2x^2+3x+4\)
\(G\left(x\right)=x^3-x^2+3x+1\)
b: \(F\left(x\right)+G\left(x\right)=2x^3+x^2+6x+5\)
\(F\left(x\right)-G\left(x\right)=3x^2+3\)
Đúng 3
Bình luận (0)
a)
F(x)=x3+2x2+3x+4F(x)=x3+2x2+3x+4
G(x)=x3−x2+3x+1
b)
F(x)+G(x)=2x3+x2+6x+5F(x)+G(x)=2x3+x2+6x+5
F(x)−G(x)=3x2+3
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình: x 3 + 2 x 2 - x - 3 2 = x - 1 x 2 - 2
x3 + 2x2 – (x – 3)2 = (x – 1)(x2 – 2)
⇔ x3 + 2x2 – (x2 – 6x + 9) = x3 – x2 – 2x + 2
⇔ x3 + 2x2 – x2 + 6x – 9 – x3 + x2 + 2x – 2 = 0
⇔ 2x2 + 8x – 11 = 0.
Có a = 2; b = 8; c = -11 ⇒ Δ’ = 42 – 2.(-11) = 38 > 0
⇒ Phương trình có hai nghiệm:
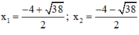
Vậy phương trình có tập nghiệm 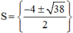
Đúng 0
Bình luận (0)
Cho các đa thức A(x)= x3 - 2x2 + 3x + 1, B(x)= x2 + x - 1 và C(x)= 2x2 - 1
a) Tính P(x)= A(x) - B(x) + C(x).
b) Tính P(0), P(-2).
a, \(P\left(x\right)=x^3-2x^2+3x+1-x^2-x+1+2x^2-1=x^3-x^2+2x+1\)
b, \(P\left(0\right)=0-0+2.0+1=0\)
\(P\left(-2\right)=-8-4-4+1=-15\)
Đúng 1
Bình luận (0)








