Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C.
QL
Những câu hỏi liên quan
Cho tam giác ABC kẻ đường cao BM và CN cắt tại H. Đường thẳng đi qua B vuông góc với BA cắt đường thẳng đi qua C vuông góc với CA tại D a, CM BH//CD, CH//BD
vì ANC = ABD =\(90^O\)Mà chúng ở vị trí đồng vị. \(\Rightarrow\)NC // BD hay CH // BD (đpcm)
vì CH // BD => HCB = CBD ( so le trong )
lại có MBC + MCB = \(90^O\)
BCD + MCB = \(90^O\)
=> MBC = BCD ( cùng phụ với MCB )
Xét tam giác HBC và tam giác DCB có :
MBC = BCD (cmt)
cạnh BC chung
HCB = CBD (cmt)
=> tam giác HBC = tam giác DCB (g - c - g)
=> HBC = BCD ( hai góc tương ứng ) mà chúng ở vị trí so le trong
=> HB // CD (đpcm)
Đúng 0
Bình luận (0)
sai rui bn oi
minh bit lam rui, du sao cung thanks ban
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC kẻ đường cao BM và CN cắt tại H. Đường thẳng đi qua B vuông góc với BA cắt đường thẳng đi qua C vuông góc với CA tại D
a, CM BH//CD, CH//BD
Ta có : BH vuông góc AC (gt)
DC vuông góc AC (gt)
=> BH//DC
C/m tương tự ta được CH//BD
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, đường cao BH, CK cắt nhau tại E. Qua B kẻ đường thẳng Bx vuông góc với AB, qua C kẻ đường thẳng Cy vuông góc với AC, Bx và Cy cắt nhau tại D.
a) Nếu DE đi qua A thì tam giác ABC là tam giác gì?
b) Tìm mối liên hệ giữa góc A và góc D của tứ giác ABCD.
Vẽ hình theo trình tự sau:- Vẽ tam giác ABC- Vẽ đường thẳng đi qua A vuông góc với BC tại H- Vẽ đường thẳng đi qua H vuông góc với AC tại T- Vẽ đường thẳng đi qua T song song với BCTrong các hình a,b,c,d dưới đây thì những hình nào vẽ đúng đề bài trên, hãy điền tên các điểm (theo đề bài) cho các hình vẽ đúng.
Đọc tiếp
Vẽ hình theo trình tự sau:
- Vẽ tam giác ABC
- Vẽ đường thẳng đi qua A vuông góc với BC tại H
- Vẽ đường thẳng đi qua H vuông góc với AC tại T
- Vẽ đường thẳng đi qua T song song với BC
Trong các hình a,b,c,d dưới đây thì những hình nào vẽ đúng đề bài trên, hãy điền tên các điểm (theo đề bài) cho các hình vẽ đúng.
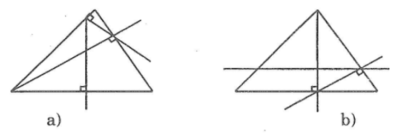
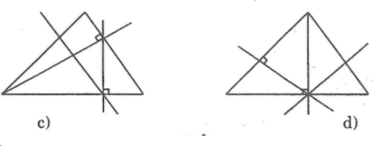
Hình a sai ; Hình b đúng ; Hình c đúng ; Hình d sai
Tên các điểm được thể hiện trong hình dưới:
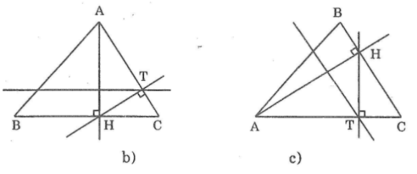
Đúng 0
Bình luận (0)
Cho tam giác ABC, vuông tại A đường cao AH. Biết AH = 2 căn 3, góc BAH = 60 độ. Tính bán kính đường tròn đi qua ba đỉnh của tam giác ABC
Xét \(\Delta\) vuông tại H \(ABH\) có :
\(tan\widehat{BAH}=tan60^o=\dfrac{BH}{AH}\Rightarrow BH=AH.tan60^o=2\sqrt[]{3}.\sqrt[]{3}=6\)
Xét \(\Delta\) vuông tại H \(ACH\) có :
\(\widehat{HAC}=90^o-\widehat{BAH}=90^o-60^o=30^o\)
\(tan\widehat{HAC}=tan30^o=\dfrac{CH}{AH}\Rightarrow CH=AH.tan30^o=2\sqrt[]{3}.\dfrac{1}{\sqrt[]{3}}=2\)
Tâm đường tròn ngoại tiếp tam giác vuông ABC là trung điểm BC
\(\Rightarrow\) Bán kính đường tròn này là :
\(R=\dfrac{BC}{2}=\dfrac{BH+CH}{2}=\dfrac{6+2}{2}=4\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn ( ) O . Gọi M là trung điểm của cạnh BC và N là điểm đối xứng của M qua O . Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D . Kẻ đường kính AE . Chứng minh rằng:b) CD đi qua trung điểm của đường cao AH của tam giác ABC .
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn ( ) O . Gọi M là trung điểm của cạnh BC và N là điểm đối xứng của M qua O . Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D . Kẻ đường kính AE . Chứng minh rằng:
b) CD đi qua trung điểm của đường cao AH của tam giác ABC .
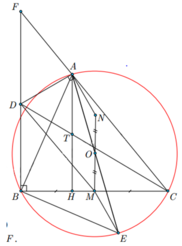
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
Đúng 0
Bình luận (0)
[ giúp mình nha ]
Cho tam giác ABC vuông tại A , AH là đường cao . D,E là hình chiếu vuông góc của H trên AB , AC .
a, Chứng mình : Tam giác ABH đồng dạng CAH
b, Chứng minh : AD.AB=AE.AC-AH
c, Chứng minh : Đường trung tuyến CM của tam giác ABC đi qua trung điểm của HE
a: Xét ΔABH và ΔCAH có
góc ABH=góc CAH
góc AHB=góc CHA
=>ΔABH đồng dạng với ΔCAH
b: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔACH vuông tại H có HE là đường cao
nên AE*AC=AH^2=AD*AB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH gọi E, F lần lượt là trung điểm AH, HC. Vẽ đường thẳng đi qua B vuông góc với AB, đường thẳng đi qua F và vuông góc với AF, chúng cắt nhau tại I. CM BEFI là hình bình hành
Cho tam giác ABC có các đường cao BK và CI cắt nhau tại H. Đường thẳng kẻ từ B vuông góc với AB và từ C vuông góc với AC cắt nhau tại D a, C/m tứ giác BHCD là hình bình hành b, Tam giác ABC thỏa mãn điều kiện gì để đường thẳng DH đi qua A. Khi đó tứ giác BICD là hình chữ nhật c, Gọi A là điểm đối xứng với A qua trung điểm M của BC . C/m góc DCA góc ACI
Đọc tiếp
Cho tam giác ABC có các đường cao BK và CI cắt nhau tại H. Đường thẳng kẻ từ B vuông góc với AB và từ C vuông góc với AC cắt nhau tại D
a, C/m tứ giác BHCD là hình bình hành
b, Tam giác ABC thỏa mãn điều kiện gì để đường thẳng DH đi qua A. Khi đó tứ giác BICD là hình chữ nhật
c, Gọi A' là điểm đối xứng với A qua trung điểm M của BC . C/m góc DCA'= góc ACI
a: Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hình bình hành
b: DH đi qua A
mà AH vuông góc BC(2)
nên DH vuông góc BC
DH đi qua A
mà DH cắt BC tại trung điểm của BC
nên AH cắt BC tại trung điểm của BC(1)
Từ (1), (2) suy ra ΔABC cân tại A
Đúng 0
Bình luận (0)



