Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn ( ) O . Gọi M là trung điểm của cạnh BC và N là điểm đối xứng của M qua O . Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D . Kẻ đường kính AE . Chứng minh rằng:
b) CD đi qua trung điểm của đường cao AH của tam giác ABC .
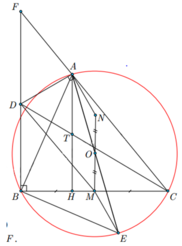
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .

