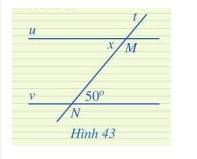
Tìm số đo x trong Hình 43, biết u // v
Bài 1: Tìm số đo x trong các hình sau, biết AB//CD.
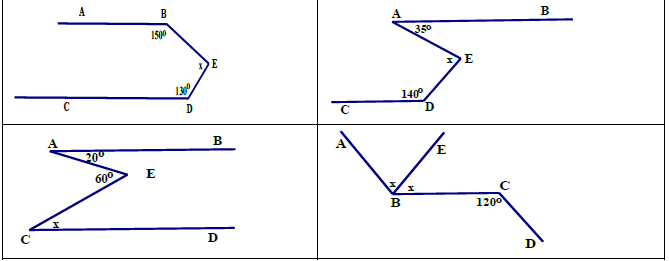
\(x=80^o\) \(x=75^o\)
\(x=20^o\) \(x=60^o\)
Vì EF//AC :
\(\Rightarrow\dfrac{BF}{BC}=\dfrac{EF}{AC}\Leftrightarrow\dfrac{2}{6}=\dfrac{3}{x}\)
\(\Leftrightarrow2x=3.6=18\)
\(\Rightarrow x=9\left(cm\right)\)
Tìm số đo x trong hình vẽ dưới đây, biết rằng 2 đường thẳng a và b song song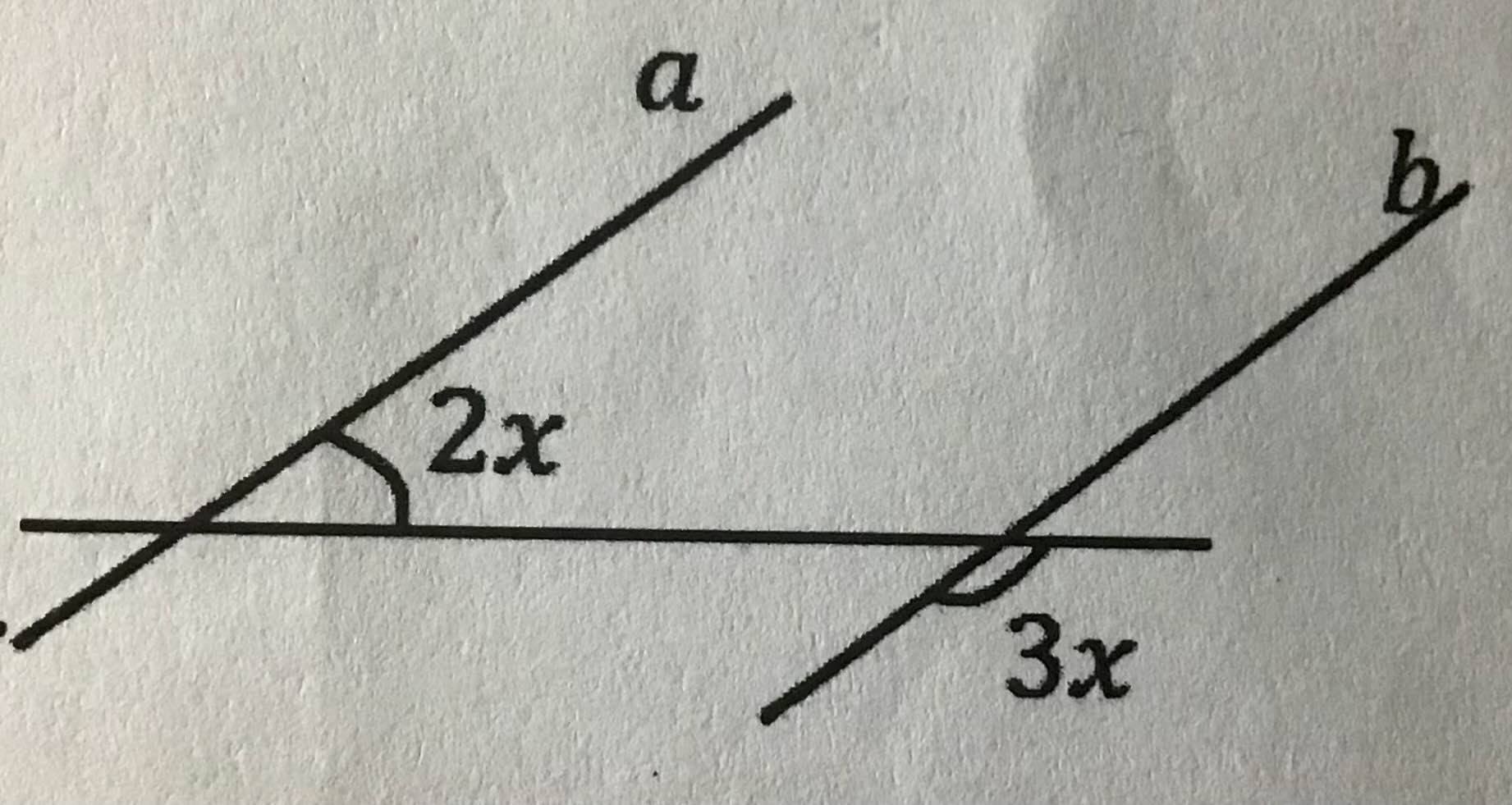
Ta có: a//b
nên \(2x+3x=180^0\)
\(\Leftrightarrow5x=180^0\)
hay \(x=36^0\)
Bài 18: a) Tìm số đo góc ACD hình
b) Tìm số đo góc IKN biết IH // MN trong hình 2 
bên trái hình 2 nha
bên phải hình 1 nha
tìm số đo x trong hình bên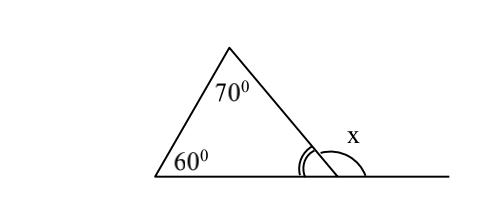
Ta có: △ABC=180o
=> góc C=180o-(70o+60o)=50o
=> C1+C2=180o
=>C2=180o-50o=130o
hay x=130o
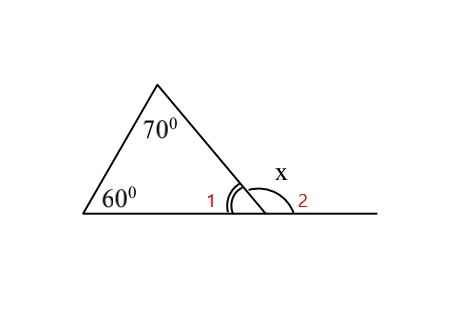
Ta chia \(\widehat{x}:\widehat{x1};\widehat{x2}\)
\(\Rightarrow\widehat{x1}=50^o\)
\(\widehat{x1}+\widehat{x2}=180^o\) (kề bù)
\(\Rightarrow\widehat{x2}=180^o-50^o=130^o\)
tìm số đo x trong hình vẽ
Ta có EMN = 1200
MNF = 600
2 góc này ở vị trí trong cùng phía và EMN + MNF = 1200 + 600 = 1800
=> a//b
Mặt khác, EFN = 900
Mà a//b
=> MEF = 900 (từ vuông góc đến song song)
Vì \(\widehat{EMN}+\widehat{MNF}=120^0+60^0=180^0\) mà 2 góc này ở vị trí trong cùng phía nên a//b
Mà \(b\perp EF\) nên \(a\perp EF\)
Do đó \(x=90^0\)
Tìm số đo x trong Hình 115.
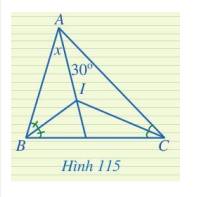
I là giao điểm của hai đường phân giác góc B và góc C.
Vậy I cũng là giao điểm của đường phân giác góc A với góc B và góc C.
Hay AI là phân giác của góc A. Vậy \(x = 30^\circ \).
Tìm số đo x trong Hình 17
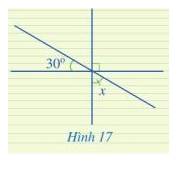
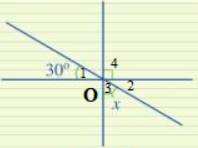
Ta có: \(\widehat {{O_1}} = \widehat {{O_2}}\) ( 2 góc đối đỉnh). Mà \(\widehat {{O_1}} = 30^\circ \Rightarrow \widehat {{O_2}} = 30^\circ \)
Ta có: \(\widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} = 180^\circ \)( kề bù)
\(\begin{array}{l} \Rightarrow x + 30^\circ + 90^\circ = 180^\circ \\ \Rightarrow x = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy x = 60\(^\circ \)
Tìm số đo x trong hình vẽ sau:
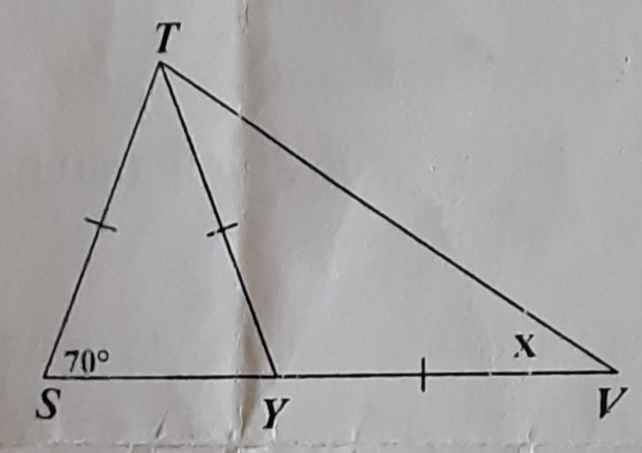
Do tam giác TSY cân tại T \(\Rightarrow\widehat{TSY}=\widehat{TYS}=70^o\)
Mà \(\widehat{TYS}\) là góc ngoài đỉnh Y của tam giác cân TVY
⇒\(2\cdot\widehat{TVY}=\widehat{TYS}=70^o\\ \Rightarrow x=35^o\)
`hat(SYT) = hat(TSY) = 70^o`
`hat(TYV) = 180^o - hat(SYT) = 180^o - 70^o = 110^o`
`=> x = (180^o - 110^o)/2 = 35^o`