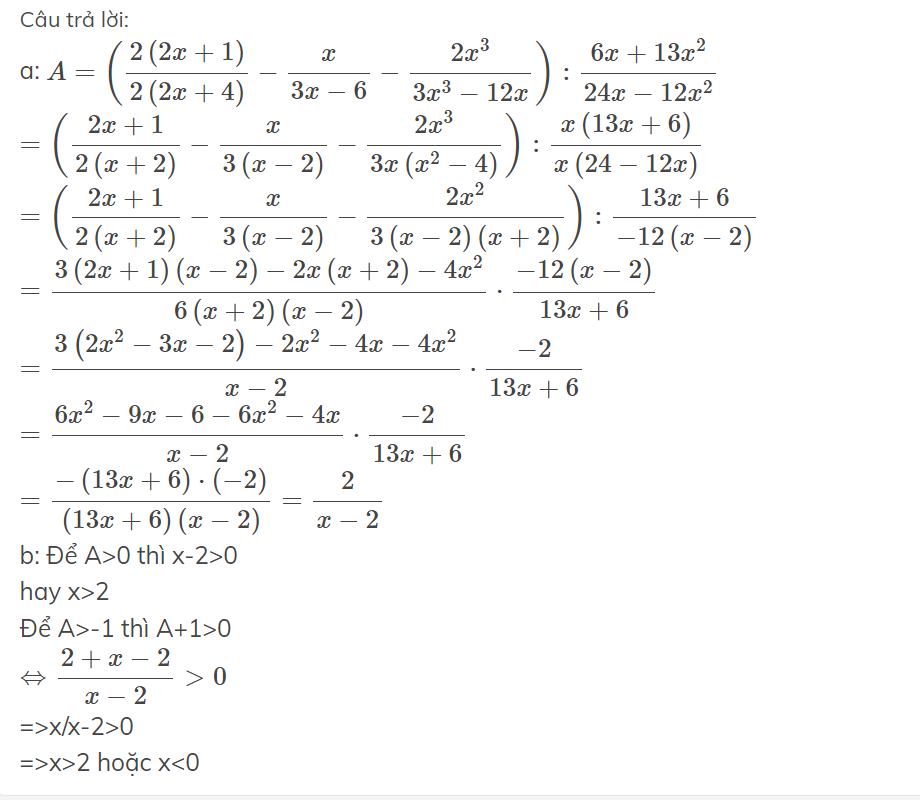Rút gọn phân thức sau: a) (3x-6)/(x^3-6x^2+12x-8) b) (x^3+2x^2)/(x^3+6x^2+12x+8)
LT
Những câu hỏi liên quan
\(A=\left(\frac{2+4x}{8+4x}-\frac{x}{3x-6}+\frac{2x^3}{12x-3x^3}\right)\div\frac{6x+13x^2}{24x-12x^2}\)
a) Tìm TXĐ và Rút gọn A
b) Tìm x để \(A>0,A>-1\)
a: \(A=\left(\dfrac{2\left(2x+1\right)}{2\left(2x+4\right)}-\dfrac{x}{3x-6}-\dfrac{2x^3}{3x^3-12x}\right):\dfrac{6x+13x^2}{24x-12x^2}\)
\(=\left(\dfrac{2x+1}{2\left(x+2\right)}-\dfrac{x}{3\left(x-2\right)}-\dfrac{2x^3}{3x\left(x^2-4\right)}\right):\dfrac{x\left(13x+6\right)}{x\left(24-12x\right)}\)
\(=\left(\dfrac{2x+1}{2\left(x+2\right)}-\dfrac{x}{3\left(x-2\right)}-\dfrac{2x^2}{3\left(x-2\right)\left(x+2\right)}\right):\dfrac{13x+6}{-12\left(x-2\right)}\)
\(=\dfrac{3\left(2x+1\right)\left(x-2\right)-2x\left(x+2\right)-4x^2}{6\left(x+2\right)\left(x-2\right)}\cdot\dfrac{-12\left(x-2\right)}{13x+6}\)
\(=\dfrac{3\left(2x^2-3x-2\right)-2x^2-4x-4x^2}{x-2}\cdot\dfrac{-2}{13x+6}\)
\(=\dfrac{6x^2-9x-6-6x^2-4x}{x-2}\cdot\dfrac{-2}{13x+6}\)
\(=\dfrac{-\left(13x+6\right)\cdot\left(-2\right)}{\left(13x+6\right)\left(x-2\right)}=\dfrac{2}{x-2}\)
b: Để A>0 thì x-2>0
hay x>2
Để A>-1 thì A+1>0
\(\Leftrightarrow\dfrac{2+x-2}{x-2}>0\)
=>x/x-2>0
=>x>2 hoặc x<0
Đúng 0
Bình luận (0)
Bài 1:Rút gọn biểu thức
a.(x-2)(2x-1)-(2x-3)(x-1)-2
b. x(x+3y+1) -2y (x-1) - (y+x+1)x
Bài 2: Tìm x
a. (14x^3 + 12x^2 -14x) :2x = (x+2) (3x-4)
b. (4x - 5) (6x+1) - (8x+3) (3x-4) =15
Bài 1.
a)
\((x-2)(2x-1)-(2x-3)(x-1)-2\\=2x^2-x-4x+2-(2x^2-2x-3x+3)-2\\=2x^2-5x+2-(2x^2-5x+3)-2\\=2x^2-5x+2-2x^2+5x-3-2\\=(2x^2-2x^2)+(-5x+5x)+(2-3-2)\\=-3\)
b)
\(x(x+3y+1)-2y(x-1)-(y+x+1)x\\=x^2+3xy+x-2xy+2y-xy-x^2-x\\=(x^2-x^2)+(3xy-2xy-xy)+(x-x)+2y\\=2y\)
Bài 2.
a)
\((14x^3+12x^2-14x):2x=(x+2)(3x-4)\\\Leftrightarrow 14x^3:2x+12x^2:2x-14x:2x=3x^2-4x+6x-8\\ \Leftrightarrow 7x^2+6x-7=3x^2+2x-8\\\Leftrightarrow (7x^2-3x^2)+(6x-2x)+(-7+8)=0\\\Leftrightarrow 4x^2+4x+1=0\\\Leftrightarrow (2x)^2+2\cdot 2x\cdot 1+1^2=0\\\Leftrightarrow (2x+1)^2=0\\\Leftrightarrow 2x+1=0\\\Leftrightarrow 2x=-1\\\Leftrightarrow x=\frac{-1}2\)
b)
\((4x-5)(6x+1)-(8x+3)(3x-4)=15\\\Leftrightarrow 24x^2+4x-30x-5-(24x^2-32x+9x-12)=15\\\Leftrightarrow 24x^2-26x-5-(24x^2-23x-12)=15\\\Leftrightarrow 24x^2-26x-5-24x^2+23x+12=15\\\Leftrightarrow -3x+7=15\\\Leftrightarrow -3x=8\\\Leftrightarrow x=\frac{-8}3\\Toru\)
Đúng 3
Bình luận (0)
Rút gọn các phân thức sau
1) \(\frac{x^2-6x+5}{4x^3-3x^2-4x+3}\)
2) \(\frac{x^2-12x-13}{6x^3+25x^2+12x-7}\)
a) Thu gọn và sắp xếp các hạng tử của đa thức sau theo lúy thừa giảm của biến
A(x)=5x^2-1/2x+8x^4-3x^2+9
b) Cho 2 đa thức
B(x)=12x^4+6x^3-1/2x+3,C(x)=-12x^4-2x^3+5x+1/2
Tính B(x)+C(x) và B(x)-C(x) tính nghiệm của đa thức K(x)=-6x+30
\(A=\left(\frac{2+4x}{8+4x}-\frac{x}{3x-6}+\frac{2x^3}{12x-3x^3}\right)\div\frac{6x+13x^2}{24x-12x^2}\)
a) Tìm TXĐ và Rút gọn A
b) Tìm x để \(A>0,A>-1\)
Cho phân thức
P=\(\frac{2x^2-8x+8}{x^3-6x^2+12x-8}\) x khác 2
a,Rút gọn P
b,Tìm tát cả các số nguyên x để P nhận giá trị nguyên
a/ \(P=\frac{2\left(x^2-4x+4\right)}{\left(x^3-8\right)-\left(6x^2-12x\right)}=\frac{2\left(x-2\right)^2}{\left(x-2\right)\left(x^2+2x+4\right)-6x\left(x-2\right)}=\frac{2\left(x-2\right)^2}{\left(x-2\right)\left(x^2-4x+4\right)}\)
\(P=\frac{2\left(x-2\right)^2}{\left(x-2\right)\left(x^2-4x+4\right)}=\frac{2\left(x-2\right)^2}{\left(x-2\right)\left(x-2\right)^2}=\frac{2}{x-2}\)
b/ Để P nguyên thì 2 phải chia hết cho x-2
=> x-2=(-2; -1; 1; 2) => x={0; 1; 3; 4}
Đúng 0
Bình luận (0)
a3 + b3 + c3 – 3abc
Ta sẽ thêm và bớt 3a2b +3ab2 sau đó nhóm để phân tích tiếp
a3 + b3 + c3 = (a3 + 3a2b +3ab2 + b3) + c3 – (3a2b +3ab2 + 3abc)
= (a + b)3 +c3 – 3ab(a + b + c)
= (a + b + c)[(a + b)2 – (a + b)c + c2 – 3ab]
= (a + b + c)(a2 + 2ab + b2 – ac – bc + c2 – 3ab]
= (a + b + c)(a2 + b2 + c2 – ab – ac – bc)
Đúng 0
Bình luận (0)
Cho phân thức
P=\(\frac{2x^2-8x+8}{x^3-6x^2+12x-8}\) x khác 2
a,Rút gọn P
b,Tìm tát cả các số nguyên x để P nhận giá trị nguyên
a)\(P=\frac{2x^2-8x+8}{x^3-6x^2+12x-8}\left(x\ne2\right)\)
\(P=\frac{2\left(x-2\right)^2}{\left(x-2\right)^3}\)
\(P=\frac{2}{x-2}\)
b)Để P nguyên thì \(2⋮x-2\).Hay \(\left(x-2\right)\inƯ\left(2\right)\)
Ư(2) là:[1,-1,2,-2]
Do đó ta có bảng sau:
| x-2 | -2 | -1 | 1 | 2 |
| x | 0 | 1 | 3 | 4 |
Đúng 0
Bình luận (0)
phân tích đa thức sau thành nhân tử
a\(12x^3y-24x^2y^2+12xy^3\)
b\(x^2-6x+xy-6y\)
c\(2x^2+2xy-x-y\)
d\(ax-2x-a^2+2a\)
e\(x^3-3x^2+3x-1\)
f\(3x^2-3y^2-12x-12y\)
b: \(x^2-6x+xy-6y\)
\(=x\left(x-6\right)+y\left(x-6\right)\)
\(=\left(x-6\right)\left(x+y\right)\)
c: \(2x^2+2xy-x-y\)
\(=2x\left(x+y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(2x-1\right)\)
e: \(x^3-3x^2+3x-1=\left(x-1\right)^3\)
Đúng 4
Bình luận (0)
Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc hiệu :
a) -x3 + 3x2 - 3x+ 1
b) 8 - 12x + 6x2 - x3
Tính giá trị của biểu thức :
a) x3 + 12x2 + 48x + 64 tại x = 6
b) x3 - 6x2 + 12x -8 tại x = 22
\(a,-x^3+3x^2-3x+1=-\left(x^3-3x^2+3x-1\right)=-\left(x^3-3.x^2.1+3.x.1^2-1^3\right)\)
\(=-\left(x-1\right)^3\)
\(b,8-12x+6x^2-x^3=2^3-3.2^2.x+3.2.x^2-x^3=\left(2-x\right)^3\)
\(a,x^3+12x^2+48x+64=x^3+3.x^2.4+3.x.4^2+4^3=\left(x+4\right)^3=\left(6+4\right)^3=10^3=1000\)
\(b,x^3-6x^2+12x-8=x^3-3.x^2.2+3.x.2^2-2^3=\left(x-2\right)^3=\left(22-2\right)^3=20^3=8000\)
Đúng 0
Bình luận (0)