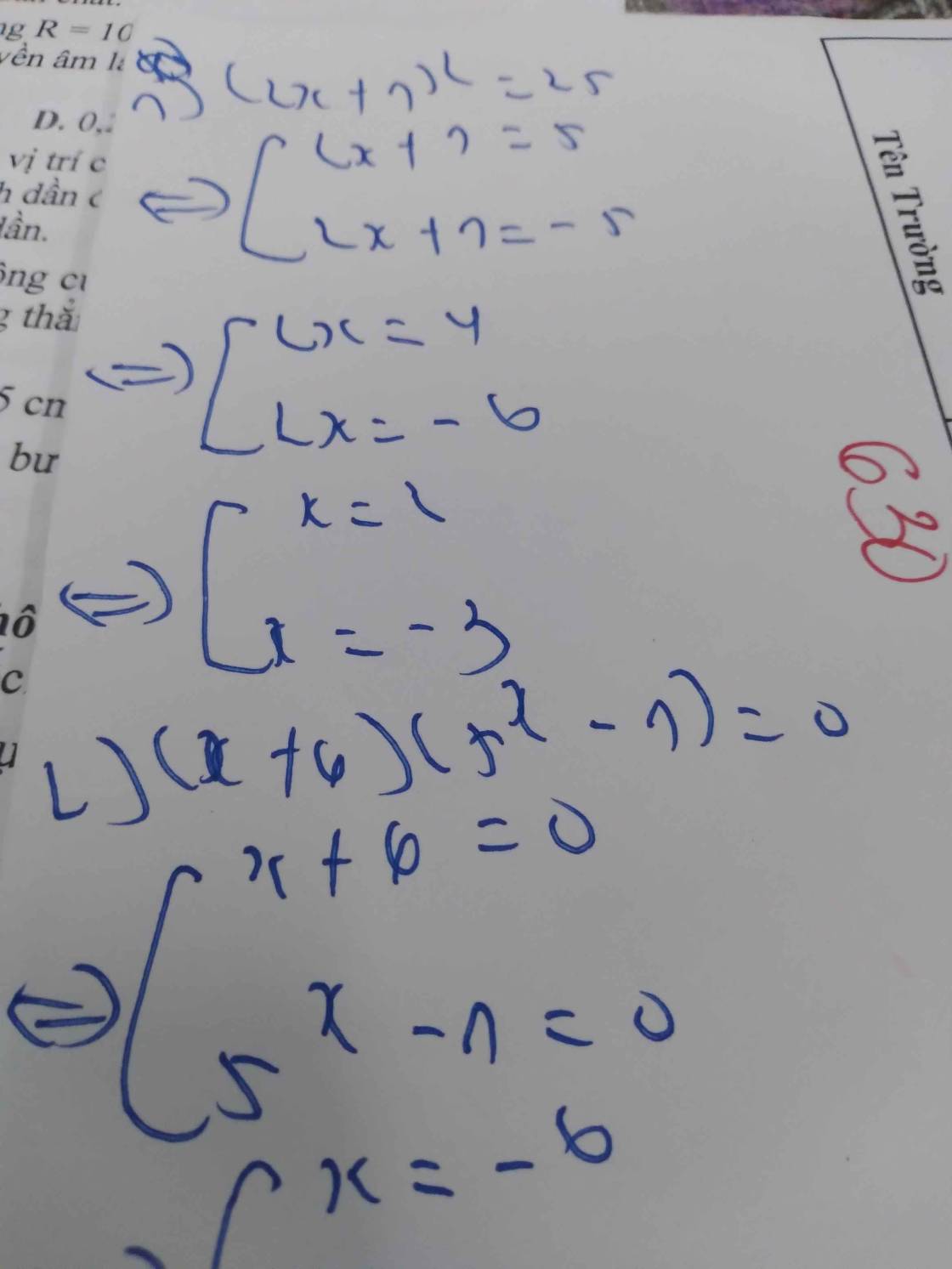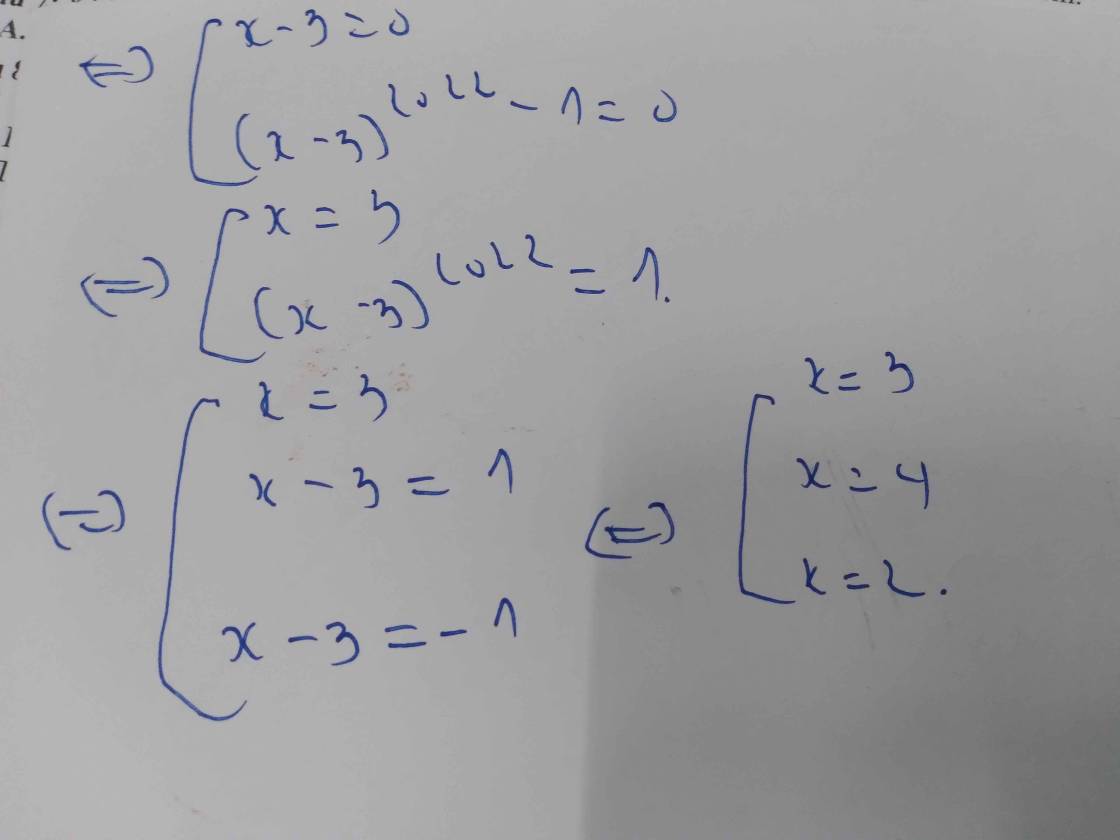Ta có : 2^x+2^{x+1}+2^{x+2}+...+2^{x+2015}=2^{2019}-82x+2x+1+2x+2+...+2x+2015=22019−8

\Leftrightarrow2^x\left(1+2+2^2+...+2^{2015}\right)=2^{2019}-8⇔2x(1+2+22+...+22015)=22019−8 (1)

Đặt : A=1+2+2^2+...+2^{2015}A=1+2+22+...+22015

\Rightarrow2A=2+2^2+2^3+...+2^{2016}⇒2A=2+22+23+...+22016

\Rightarrow2A-A=\left(2+2^2+2^3+...+2^{2016}\right)-\left(1+2+2^2+...+2^{2015}\right)⇒2A−A=(2+22+23+...+22016)−(1+2+22+...+22015)

\Rightarrow A=2^{2016}-1⇒A=22016−1

Khi đó (1) trở thành :

2^x\left(2^{2016}-1\right)=2^{2019}-2^32x(22016−1)=22019−23

$\iff 2$

xin lỗi, bạn vào trang cá nhân của mình xem nhé, mik đang vội nha, mik gửi mà nó ko lên ạ

$2^x+2^{x+1}+...+2^{x+2015}=2^{2019}-8$

$\to 2^x.1+2^x.2+....+2^x.2^{2015}=2^{2019}-8$

$\to 2^x.(1+2+...+2^{2015})=2^{2019}-8$

Đặt:

$A=1+2+...+2^{2015}$

$2A=2.(1+2+...+2^{2015})$

$2A=2+2^2+...+2^{2016}$

\(B=2^2+2^3+2^4+...+2^{121}\\=(2^2+2^3)+(2^4+2^5)+(2^6+2^7)+...+(2^{120}+2^{121})\\=2^2\cdot(1+2)+2^4\cdot(1+2)+2^6\cdot(1+2)+...+2^{120}\cdot(1+2)\\=2^2\cdot3+2^4\cdot3+2^6\cdot3+...+2^{120}\cdot3\\=3\cdot(2^2+2^4+2^6+...+2^{120})\)

Vì \(3\cdot(2^2+2^4+2^6+...+2^{120})\vdots3\)

nên \(B\vdots3\)

\(A=2^0+2^1+2^2+2^3+2^4+2^5+\dots+2^{100}\\=(2^1+2^2)+(2^3+2^4)+(2^5+2^6)+\dots+(2^{99}+2^{100})+2^0\\=2\cdot(1+2)+2^3\cdot(1+2)+2^5\cdot(1+2)+\dots+2^{99}\cdot(1+2)+1\\=2\cdot3+2^3\cdot3+2^5\cdot3+\dots+2^{99}\cdot3+1\\=3\cdot(2+2^3+2^5+\dots+2^{99})+1\)

Vì \(3\cdot(2+2^3+2^5+\dots+2^{99})\vdots3\)

\(\Rightarrow 3\cdot(2+2^3+2^5+\dots+2^{99})+1\) chia \(3\) dư 1

hay số dư của phép chia \(A\) cho \(3\) là \(1\).

A=2^0 + 2^1 + 2^2 + 2^3 + 2^4 + ....+2^100

A=1 + 2^1 + 2^2 + 2^3 + 2^4 + ....+2^100

A=1 + (2^1 + 2^2) + (2^3 + 2^4) + ....+(2^99 + 2^100)

A=1 + 2.(1+2) + 2^3.(1+2)+....+2^99.(1+2)

A=1 + 2 . 3 + 2^3 . 3 +....+2^99 . 3

A=1 +3 .(2+2^3+..+2^99)

=> A:3 dư 1

a)<=>

A,=(x+y)(x-y)=x^2-y^2

x=(-1/2)^5:(1/2)^4=-1/2

x^2=1/4

y=8^2/(-2)^5=-2

y^2=4

A=1/4-4=-15/4

a) \(1,25^2-0,5^2+3,25^3\)

\(=\left(\frac{5}{4}\right)^2-\left(\frac{1}{2}\right)^2+\left(\frac{13}{4}\right)^3\)

\(=\frac{25}{16}-\frac{1}{4}+\frac{2197}{64}\)

\(=\frac{2281}{64}\)

b) \(1,2+2,4^2-\left(3\frac{1}{2}\right)^2\)

\(=\frac{6}{5}+\left(\frac{12}{5}\right)^2-\left(\frac{7}{2}\right)^2\)

\(=\frac{6}{5}+\frac{144}{25}-\frac{49}{4}\)

\(=\frac{-529}{100}\)

`(2^x+1)^2 =25`

`=> (2^x+1)^2 = (+-5)^2`

\(\Rightarrow\left[{}\begin{matrix}2^x+1=5\\2^x+1=-5\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}2^x=4\\2^x=-6\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)

\(\left(x+6\right)\left(5^x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x+6=0\\5^x-1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-6\\5^x=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=0\end{matrix}\right.\)

\(\left(x-3\right)^{2023}=x-3\)

\(\Rightarrow\left(x-3\right)^{2023}-\left(x-3\right)=0\)

\(\Rightarrow\left(x-3\right)\left[\left(x-3\right)^{2022}-1\right]=0\)

\(\Rightarrow\left[{}\begin{matrix}x-3=0\\\left(x-3\right)^{2022}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x-3=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)

`#3107.101107`

1.

`(2^x + 1)^2 = 25`

`=> (2^x + 1)^2 = (+-5)^2`

`=>`\(\left[{}\begin{matrix}2^x+1=5\\2^x+1=-5\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}2^x=4\\2^x=-6\left(\text{vô lý}\right)\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)

Vậy, `x =2.`

2.

`(x + 6)(5x - 1) = 0`

`=>`\(\left[{}\begin{matrix}x+6=0\\5x-1=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=-6\\5x=1\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=-6\\x=\dfrac{1}{5}\end{matrix}\right.\)

Vậy, `x \in {-6; 1/5}`

3.

`2*3^(x + 3) + 3^(2 + x) = 891`

`=> 2* 3^x * 3^3 + 3^2 * 3^x = 891`

`=> 54*3^x + 9*3^x = 891`

`=> 3^x * (54 + 9) = 891`

`=> 3^x * 63 = 891`

`=> 3^x = 891 \div 63`

`=> 3^x = 891/63`

Bạn xem lại đề.

4.

`(x - 3)^2023 = x - 3`

`=> (x - 3)^2023 - (x - 3) = 0`

`=> (x - 3) * [ (x - 3)^2022 - 1] = 0`

`=>`\(\left[{}\begin{matrix}x-3=0\\\left(x-3\right)^{2022}-1=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=1\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=\left(\pm1\right)^{2022}\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=3\\x-3=1\\x-3=-1\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=3\\x=4\\x=2\end{matrix}\right.\)

Vậy, `x \in {2; 3; 4}.`

Thay \(x=\dfrac{1}{2}\) vào A, ta được:

\(A=3\cdot\left(\dfrac{1}{2}\right)^2-2\cdot\dfrac{1}{2}+1=\dfrac{3}{4}-1+1=\dfrac{3}{4}\)