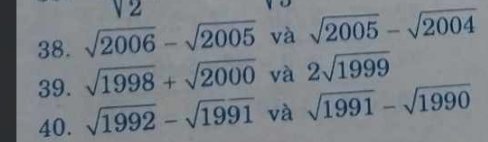 giúm mình bài này v ạ so sánh ạ mình camon
giúm mình bài này v ạ so sánh ạ mình camon
HT
Những câu hỏi liên quan

giúm mình làm bài này với ạ
Giải giúm mình với ạ .Gấp ạ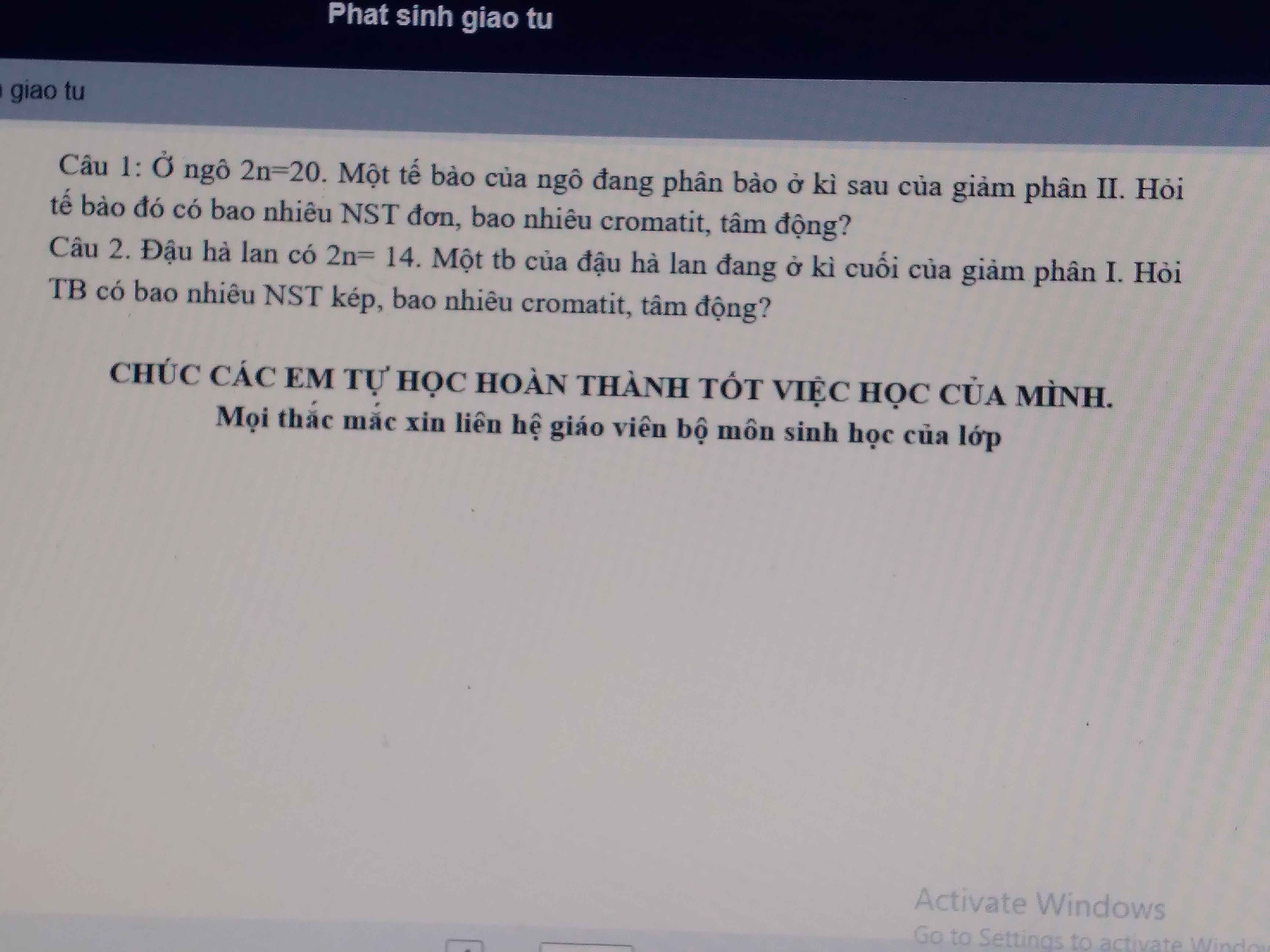
Câu 1 : Ở ngô 2n = 20
Kì sau giảm phân II
- Số NST đơn : 2n =20
- Số cromatit : 0
- Số tâm động : 20
Câu 2: Đậu Hà lan : 2n = 14
Kì cuối GPI
- Số NST kép : n = 7
- Số cromatit: 14
- Số tâm động: 7
Đúng 0
Bình luận (0)
Mọi ngừi ơi cho mình hỏi bài này ạ mình đag cần gấp : ( Gạch thẳng là giá trị tuyệt đối ) :7 /2 - gạch thẳng 2x-3/4 gạch thẳng = -7/4 Camon trước ạ
\(\frac{7}{2}\)-\(|\frac{2x-3}{4}\)\(|\)=\(\frac{-7}{4}\)
\(|\frac{2x-3}{4}|\)=\(\frac{7}{2}\)+\(\frac{7}{4}\)
\(|\frac{2x-3}{4}|\)=\(\frac{21}{4}\)
=>\(|2x-3|\)=\(21\)
=>2x-3=21 hay 2x-3=-21
2x=21+3 2x=-21+3
2x=24 2x=-18
x=12 x=-9
so sánh -3 mũ 150 và -2 mũ 225
mn bày mình bài này làm sao đi ạ :(((
\(-3^{150}=-9^{75}\)
\(-2^{225}=-8^{75}\)
mà -9<-8
nên \(-3^{150}< -2^{225}\)
Đúng 1
Bình luận (1)
ta có : -3^150 = (-3^2)^75= -6^75
-2^225 = (-2^3)^75=-6^75
Do 6^75 = 6^75 nên -3^150 = 2^225
Đây là cách của thầy mik dạy
Mik ko bt có đúng hay ko đâu :(
Đúng 0
Bình luận (1)
 giúp mình câu 11 , 12 v ạ mình camon
giúp mình câu 11 , 12 v ạ mình camon
11) \(\dfrac{2\sqrt{3}-\sqrt{15}}{\sqrt{3}}\)
\(=\dfrac{\left(2\sqrt{3}-\sqrt{15}\right)\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}\)
\(=\dfrac{2\cdot\sqrt{3}\cdot\sqrt{3}-\sqrt{15}\cdot\sqrt{3}}{3}\)
\(=\dfrac{6-3\sqrt{5}}{3}\)
\(=2-\sqrt{5}\)
12) \(\dfrac{2\sqrt{2}+\sqrt{2}}{5\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{5\sqrt{2}}\)
\(=\dfrac{3}{5}\)
Đúng 2
Bình luận (0)
11: \(=\dfrac{\sqrt{3}\left(2-\sqrt{5}\right)}{\sqrt{3}}=2-\sqrt{5}\)
12: \(=\dfrac{3\sqrt{2}}{5\sqrt{2}}=\dfrac{3}{5}\)
Đúng 1
Bình luận (0)

giải chi tiết và giải thích rõ ràng giúm mình ạ, mình phải nộp trước 9h sáng mai ạ
Giải hộ mình bài này với:
So sánh: 5 mũ 143 và 7 mũ 95
Cảm ơn ạ!
so sánh (100^10+1)/(100^10-1) với (10^100+1)/(10^100-3)
giúp mình bài này với ạ
đặt A=100^10+1/100^10-1
B=10^100+1/10^100-3
ta có:\(A=\frac{100^{10}+1}{100^{10}-1}=\frac{100^{10}-1+2}{100^{10}-1}=\frac{100^{10}-1}{100^{10}-1}+\frac{2}{100^{10}-1}=1+\frac{2}{100^{10}-1}\)
\(B=\frac{10^{100}+1}{10^{100}-3}=\frac{10^{100}-3+4}{10^{100}-3}=\frac{10^{100}-3}{10^{100}-3}+\frac{4}{10^{100}-3}=1+\frac{4}{10^{100}-3}=1+\frac{4}{100^{10}-3}\)
vì 10010-1>10010-3
=>\(\frac{4}{100^{10}-1}<\frac{4}{100^{10}-3}\)
=>A<B
Đúng 0
Bình luận (0)
Ta có:
\(\frac{100^{10}+1}{100^{10}-1}=\frac{100^{10}-1+2}{100^{10}-1}=\frac{100^{10}-1}{100^{10}-1}+\frac{2}{100^{10}-1}=1+\frac{2}{10^{20}-1}=1+\frac{4}{2.10^{20}-2}\)
\(\frac{10^{100}+1}{10^{100}-3}=\frac{10^{100}-3+4}{10^{100}-3}=\frac{10^{100}-3}{10^{100}-3}+\frac{4}{10^{100}-3}=1+\frac{4}{10^{100}-3}=1+\frac{4}{10^{100}-3}\)
Thấy: \(2.10^{20}-2<10^{100}-3\)
\(\Rightarrow\frac{4}{2.10^{20}-1}>\frac{4}{10^{100}-3}\)
\(\Rightarrow\frac{100^{10}+1}{100^{10}-1}>\frac{10^{100}+1}{10^{100}-3}\)
Đúng 0
Bình luận (0)
giúp mình bài này vs ạ
bài 1:so sánh các căn sau
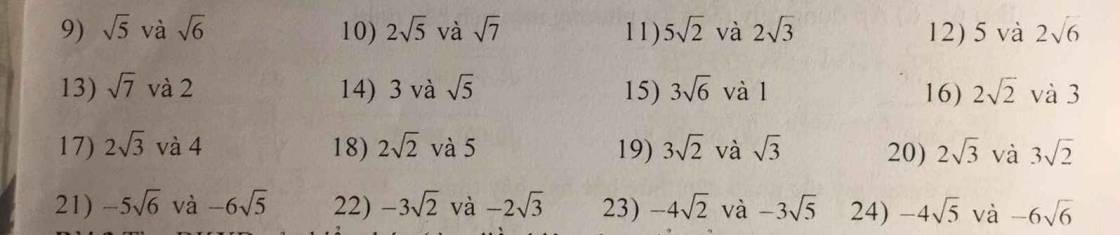
bài 2 :tìm ĐKXĐ của biểu thức (tìm đk của x để biểu thức sau có nghĩa)
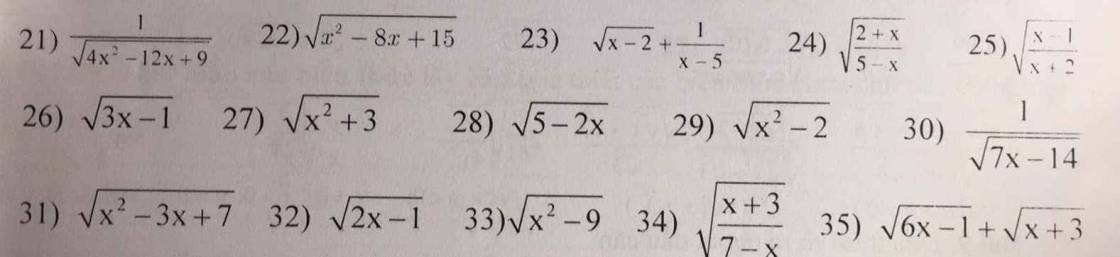
Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Đúng 2
Bình luận (0)
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)
Đúng 2
Bình luận (0)
Chỉ đăng tối đa 10 - 15 câu hỏi thôi, câu trước GV nhắc bạn rồi mà giờ bạn vẫn còn đăng nữa thì nên bị xóa câu hỏi.
Đúng 1
Bình luận (3)
Xem thêm câu trả lời






