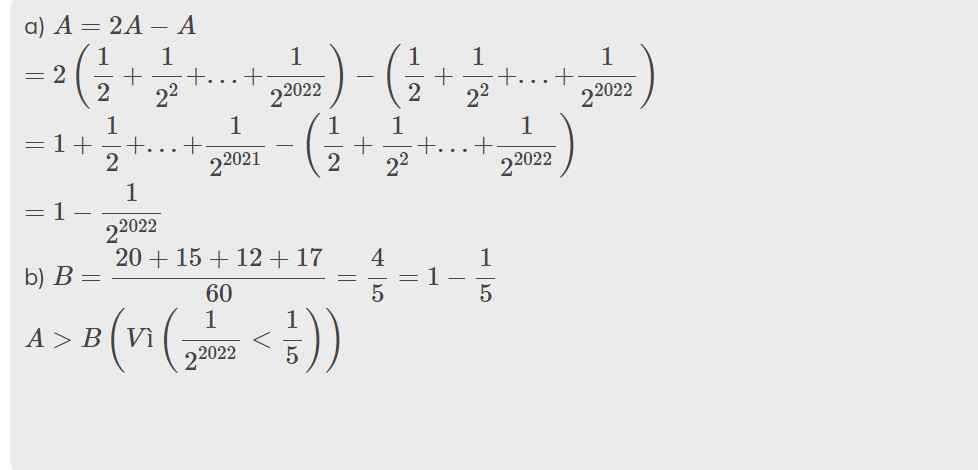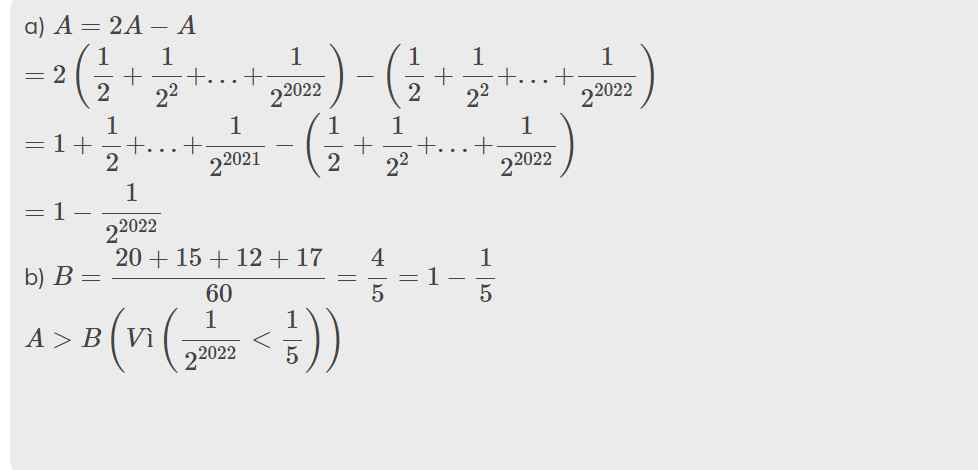A = 1 + 2+22 + 23 .....+22020, so sánh A với 22021
PM
Những câu hỏi liên quan
Cho A =2+22+23+.....+22020+22021+22022
CHỨNG TỎ rằng A chia hết cho3
\(A=2+2^2+2^3+...+2^{2020}+2^{2021}+2^{2022}\\=(2+2^2)+(2^3+2^4)+(2^5+2^6)+...+(2^{2021}+2^{2022})\\=2\cdot(1+2)+2^3\cdot(1+2)+2^5\cdot(1+2)+...+2^{2021}\cdot(1+2)\\=2\cdot3+2^3\cdot3+2^5\cdot3+...+2^{2021}\cdot3\\=3\cdot(2+2^3+2^5+..+2^{2021})\)
Vì \(3\cdot\left(2+2^3+2^5+...+2^{2021}\right)⋮3\)
nên \(A⋮3\).
\(Toru\)
Đúng 0
Bình luận (0)
A=(2+22)+22(2+22)+...+22020(2+22)
A= 6.1+22.6+...+22020.6
A=6(1+22+...+22020) chia hết cho 3
vậy A chia hết cho 3
Đúng 0
Bình luận (0)
A=(2+22)+(23+24)+(25+26)+.......+(22019+22020)+(22021+22022)
A=2.(1+2)+23.(1+2)+25.(1+2)+.......+22019.(1+2)+22021.(1+2)
A=2.3+23.3+25.3+.......+22019.3+22021.3
A=3.(2+23+25+........+22019+22021)
Vì 3⋮3⇒A⋮3
Đúng 0
Bình luận (0)
so sánh:
A=1/2+1/22+1/23+...+1/22020+1/22021 và B=1/3+1/4+1/5+13/60
A=1/2+1/22+1/23+...+1/22020+1/22021 > B=1/3+1/4+1/5+13/60
Đúng 1
Bình luận (0)
giải bài toán gúp em em sắp thi hcoj kì ạ
Cho A = 1 + 2 + 22 + … + 22020 và B = 22021 – 1
So sánh A và B.
nhanh nhanh nhanh nhanh nhanh nhanh nhanh nhanh
Đúng 0
Bình luận (0)
\(A=1+2+2^2+...+2^{2020}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{2021}\)
\(\Rightarrow2A-A=2+2^2+2^3+...+2^{2021}-1-2-2^2-...-2^{2020}\)
\(\Rightarrow A=2^{2021}-1\)
\(\Rightarrow A=2^{2021}-1=B\)
Đúng 1
Bình luận (0)
M=1+2+22+23+24+…+22020+22021. Chững minh M chia hết cho 3.
Các bạn giúp mình với nha.Cảm ơn!
A=1+2+22+....+22020+22021
A = 1 + 2 + 22 + ... + 22021
2A = 2 + 4 + 23 + ... 22022
A = 22022 - 1
Đúng 1
Bình luận (0)
\(A=1+2+2^2+...+2^{2020}+2^{2021}\)
\(2A=2+2^2+2^3+...+2^{2021}+2^{2022}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2021}+2^{2022}\right)-\left(1+2+2^2+...+2^{2020}+2^{2021}\right)\)
\(A=2^{2022}-1\)
Đúng 1
Bình luận (0)
1/2 + 1/22+1/23+...+1/22020+1/22021=?
mình đang gấp lắm, mong các bạn giải dùm
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\)
\(\Rightarrow\dfrac{1}{2}A=\dfrac{1}{2}.\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\right)\)\(\Rightarrow\dfrac{1}{2}A=\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\)
\(\Rightarrow A-\dfrac{1}{2}A=\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\right)\)\(\Rightarrow\dfrac{1}{2}A=\dfrac{1}{2}-\dfrac{1}{2^{2022}}\)
\(\Rightarrow\dfrac{1}{2}A=\dfrac{2^{2021}-1}{2^{2022}}\)
\(\Rightarrow A=\dfrac{2^{2021}-1}{2^{2023}}.2=\dfrac{2^{2021}-1}{2^{2021}}\)
Vậy \(A=\dfrac{2^{2021}-1}{2^{2021}}\)
Đúng 0
Bình luận (0)
A=1+2+22+...+22020 +22021 và B= 22022 chứng minh Avà B là số tự nhiên liên tiếp
\(A=1+2+2^2+...+2^{2020}+2^{2021}\\ \Rightarrow2A=2+2^2+2^3+...+2^{2021}+2^{2022}\\ \Rightarrow2A-A=A=2^{2022}-1\)
Vậy \(A\) và \(B\) là 2 số tự nhiên liên tiếp.
Đúng 2
Bình luận (1)
A = 1/2 + 1/22 + 1/23 + 1/24+...+ 1/22021 + 1/22022
và B = 1/3+1/4+1/5+17/60
Hỏi :
a) Rút gọn A
b)So sánh A và B
so sánh P và Q biết
1+2+22+23 + ....... +22021 và Q = 2022
\(2P=2+2^2+2^3+...+2^{2022}\)
\(\Leftrightarrow P=2^{2022}-1< Q\)
Đúng 0
Bình luận (0)