chỉ mình bài này với:

Chỉ giúp mình bài này với
C4:
A + O2 --- > CO2 + H2O
nCO2 = 4,4/44 = 0,1 (mol)
=> nC = 0,1 (mol)
=> nO = 2nCO2 = 2.0,1 = 0,2 (mol) (1)
nH2O = 1,8/18 = 0,1 (mol)
=> nH = 0,1.2 = 0,2 (mol)
=> nO = 0,1 (mol ) (2)
BTKL : mA + mO2 = mCO2 + mH2O
2,2 + mO2 = 4,4 + 1,8
=> mO2 = 4 (g)
=> nO2 = 4/32 = 0,125 (mol)
=> nO = 0,125 . 2 = 0,25 (mol) (3)
=> nO(trong A ) = nO(1) + nO(2) - nO(3) = 0,2 + 0,1 - 0,25 = 0,05 (mol)
=> A gồm có các nguyên tố : C;H và O
Gọi CTHH dạg chung của A là CxHyOz
Ta có : x:y:z = 0,1 : 0,2 : 0,05 = 2 : 4 : 1
Vậy CTPT của A là C2H4O
Chỉ mình bài này với ạ🥺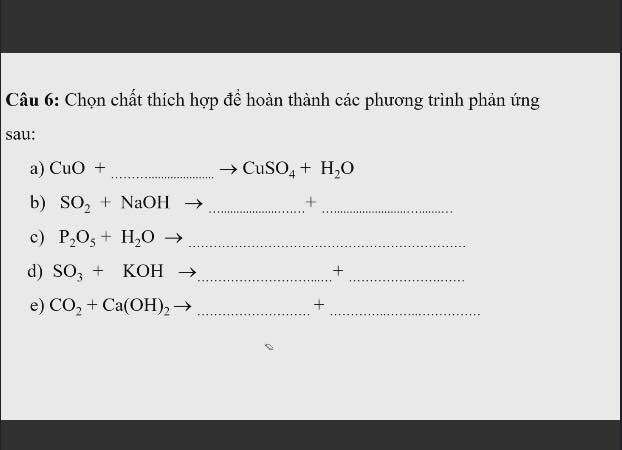
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
\(SO_2+2NaOH\rightarrow Na_2SO_3+H_2O\)
\(P_2O_5+3H_2O\rightarrow2H_3PO_4\)
\(SO_3+2KOH\rightarrow K_2SO_4+H_2O\)
\(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
Chỉ mình bài này với ak🥺
chỉ mình 2 bài này với ạ
Chỉ mình mấy bài này với, hứa vote
Câu 3.
\(R_Đ=\dfrac{U^2_Đ}{P_Đ}=\dfrac{220^2}{110}=440\Omega\)
\(R_b=\dfrac{U^2_b}{P_b}=\dfrac{220^2}{440}=110\Omega\)
\(R_{tđ}=\dfrac{R_Đ\cdot R_b}{R_Đ+R_b}=\dfrac{440\cdot110}{440+110}=88\Omega\)
\(I_m=\dfrac{U}{R}=\dfrac{220}{88}=2,5A\)
Câu 4.
\(R_{tđ}=R_1+R_2=20+40=60\Omega\)
Để hai điện trở chịu đc 1 hđt thích hợp thì cần một dòng điện phù hợp qua chúng.
\(\Rightarrow I_m=I_{min}=1,5A\)
\(\Rightarrow U_m=60\cdot1,5=90V\)
Uhm, bạn cần bài nào thì chụp bài đó nhé! Với lại khi đăng bạn nhớ quay hình lại để người giải dễ nhìn, cách bạn đăng dễ nhìn sẽ khiến người giải có cảm tình để giúp nhé!
 mọi người ơi chỉ mình bài này với
mọi người ơi chỉ mình bài này với
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình thoi}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
\(\widehat{D}=\widehat{B}=60^0\Rightarrow\Delta ACD\) đều
Đường thẳng \(AO\) cắt (SCD) tại C, mà \(OC=\dfrac{1}{2}AC\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}d\left(A;\left(SCD\right)\right)\)
Gọi M là trung điểm CD \(\Rightarrow AM\perp CD\) (do tam giác ACD đều)
\(\Rightarrow CD\perp\left(SAM\right)\)
Từ A kẻ \(AH\perp SM\Rightarrow AH\perp\left(SCD\right)\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(AM=\dfrac{AD\sqrt{3}}{2}=?\) (đến đây thì nhận ra bạn chép đề bài thiếu, hình thoi chưa biết độ dài cạnh)
Áp dụng hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}\Rightarrow AH=\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=?\)
\(\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}AH=?\)
Ai ơi, chỉ mình làm bài này với !!!!! (=_=) ^(*-*)^
CHỈ MÌNH CÁCH LÀM BÀI NÀY VỚI Ạ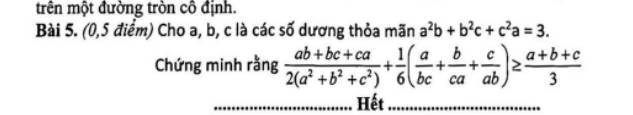
Ta có:
\(\dfrac{ab+bc+ca}{2\left(a^2+b^2+c^2\right)}+\dfrac{1}{6}\left(\dfrac{a^2+b^2+c^2}{abc}\right)\ge2\sqrt{\dfrac{1}{12}\left(\dfrac{ab+ca+ca}{abc}\right)}=\sqrt{3\left(\dfrac{ab+bc+ca}{abc}\right)}\)
Nên ta chỉ cần cm:
\(\sqrt{\dfrac{1}{3}\left(\dfrac{ab+bc+ca}{abc}\right)}\ge\dfrac{a+b+c}{3}\Leftrightarrow3\left(\dfrac{ab+bc+ca}{abc}\right)\ge\left(a+b+c\right)^2\)
Thật vậy, ta có:
\(\dfrac{3\left(ab+bc+ca\right)}{abc}=\dfrac{\left(a^2b+b^2c+c^2a\right)\left(ab+bc+ca\right)}{abc}\)
\(=\left(\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{c}{b}\right)\left(ac+ab+bc\right)\ge\left(a+b+c\right)^2\) (Bunhiacopxki)
Dấu "=" xảy ra khi \(a=b=c=1\)