Đề:Câu 4 (3,0 điểm) Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.a) Chứng minh tứ giác AOBF nội tiếp b) Chứng minh I là trung điểm của KGCâu 4 (3,0 điểm)Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA vàFB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE c...
Đọc tiếp
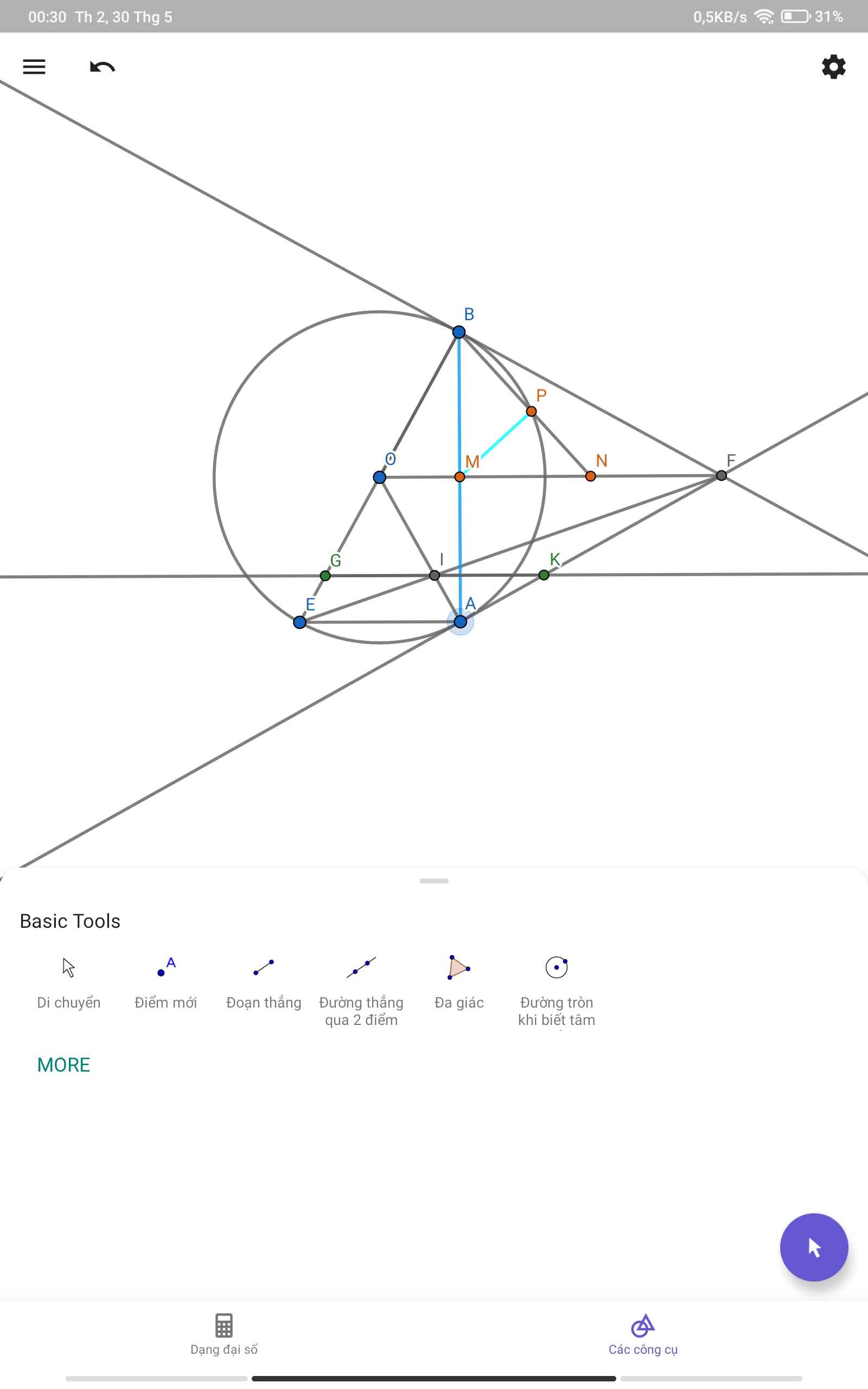
Đề:Câu 4 (3,0 điểm) Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KGCâu 4 (3,0 điểm)
Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và
FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE
cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại
P ( P khác B). Chứng minh PM vuông góc với NBc) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại P ( P khác B). Chứng minh PM vuông góc với NB —->Giải câu b và c thôi nha