Trong mặt phẳng Oxy cho tam giac ABC có A(2;1);B(1;-5);C(3;2) a) Viết phương trình tổng quát của đường cao AH của tam giac ABC. b) Viết phương trình đường tron có tâm I(3;1) và Đi qua điểm B.
YN
Những câu hỏi liên quan
Trong mặt phẳng tọa độ oxy, cho tam giac abc vuong tai co dinh b(-3;2), duong phan giac trong goc a co phuong trinh x+y-7=0. viet phuong trinh duong tron noi tiep tam giac abc, biet dien tich tam giac abc bang 24 va a co hoanh do duong
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(-4;1), B(-1;4), C(3;-2) Tìm tọa độ trực tâm của tam giác ABC
trong mặt phẳng tọa độ oxy cho tam giác ABC có A(2;3); B ( -3;1);C (0;-1) .tìm tọa độ các đỉnh cua tam giac MNP sao cho A,B,C lan luot la trung diem cua cac canh MN,NP,PM
Trong mặt phẳng Oxy, cho tam giác ABC có A=(-2:3), B=(1:-2), C=(-5:4). Lập phương trình đường phân giác trong của góc ABC
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0; 2), B(-2; 8), C(-3; 1). Tọa độ tâm đường tròn ngoại tiếp của tam giác ABC là
A.( 5/2; -9/2)
B.(- 5/2; 9/2)
C.(-2; 4)
D. (-3;5)
Gọi I(a; b) là tâm đường tròn ngoại tiếp tam giác ABC.
A I 2 = B I 2 A I 2 = C I 2 ⇔ a − 0 2 + b − 2 2 = a + 2 2 + b − 8 2 a − 0 2 + b − 2 2 = a + 3 2 + b − 1 2
⇔ a 2 + b 2 − 4 b + 4 = a 2 + 4 a + 4 + b 2 − 16 b + 64 a 2 + b 2 − 4 b + 4 = a 2 + 6 a + 9 + b 2 − 2 b + 1
4 a − 12 b = − 64 6 a + 2 b = − 6 ⇔ a − 3 b = − 16 3 a + b = − 3
⇔ a = − 5 2 b = 9 2
Chọn B.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;2), B(2;3), C(-3;-4). Diện tích tam giác ABC bằng A. 1. B.
2
C.
1
+
2
D.
3
2
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;2), B(2;3), C(-3;-4). Diện tích tam giác ABC bằng
A. 1.
B. 2
C. 1 + 2
D. 3 2
Trong mặt phẳng oxy cho tam giác abc biết A(-1;1),B(3;-2),C(5;1). Tính chu vi Tam giác abc
\(\overrightarrow{AB}=\left(4;-3\right)\Rightarrow AB=5\)
\(\overrightarrow{AC}=\left(6;0\right)\Rightarrow AC=6\)
\(\overrightarrow{BC}=\left(2;3\right)\Rightarrow BC=\sqrt{13}\)
Chu vi tam giác: \(AB+AC+BC=11+\sqrt{13}\)
Đúng 2
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;-1), B(4;5) và C(-3;2). Lập phương trình đường cao của tam giác ABC kẻ từ A.
A. 7x + 3y - 11 = 0
B. -3x + 7y + 13 = 0
C. 3x + 7y + 1 = 0
D. 7x + 3y + 13 = 0
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2) 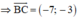
Phương trình đường cao AH đi qua A(2;-1) nhận 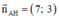 là VTPT là:
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4); B(3; 2); C(5; 4). Tính chu vi P của tam giác đã cho. A.
P
4
+
2
2
.
B.
P
4
+
4
2
.
C.
P
8
+
8
2
.
D.
P
2
+
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4); B(3; 2); C(5; 4). Tính chu vi P của tam giác đã cho.
A. P = 4 + 2 2 .
B. P = 4 + 4 2 .
C. P = 8 + 8 2 .
D. P = 2 + 2 2 .
Ta có A B → = 2 ; − 2 B C → = 2 ; 2 C A → = − 4 ; 0 ⇒ A B = 2 2 + − 2 2 = 2 2 B C = 2 2 + 2 2 = 2 2 C A = − 4 2 + 0 2 = 4
Vậy chu vi P của tam giác ABC là P =AB + BC + CA = 4 + 4 2
Chọn B.
Đúng 0
Bình luận (0)


