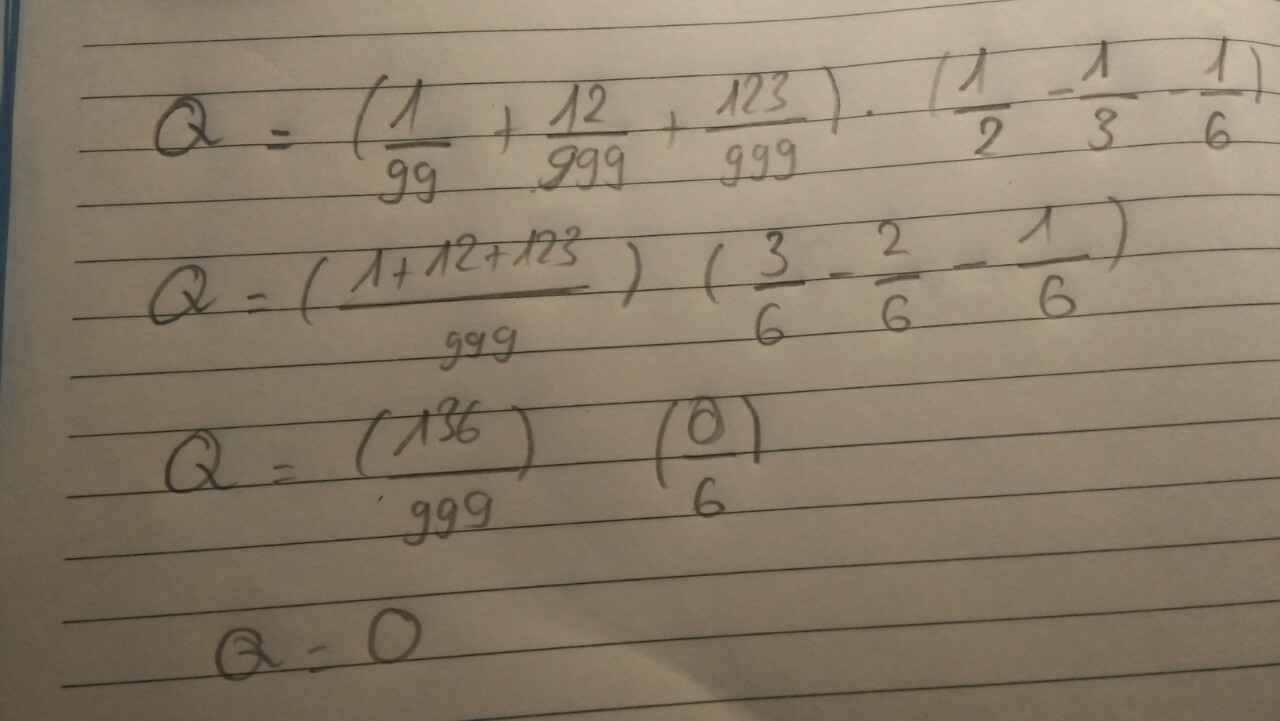tính giá trị biểu thức \(\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+.....+\dfrac{1}{9900}\)
DM
Những câu hỏi liên quan
Tính giá trị biểu thức sau bằng cách thuận tiện nhất và kết quả dưới dạng số thập phân1dfrac{1}{10}+1dfrac{4}{20}+1dfrac{9}{30}+1dfrac{16}{40}+1dfrac{25}{50}+1dfrac{36}{60}+1dfrac{49}{70}+1dfrac{64}{80}+1dfrac{81}{90}giúp mik với mik cần gấp
Đọc tiếp
Tính giá trị biểu thức sau bằng cách thuận tiện nhất và kết quả dưới dạng số thập phân
\(1\dfrac{1}{10}\)+\(1\dfrac{4}{20}\)+\(1\dfrac{9}{30}\)+\(1\dfrac{16}{40}\)+\(1\dfrac{25}{50}\)+\(1\dfrac{36}{60}\)+\(1\dfrac{49}{70}\)+\(1\dfrac{64}{80}\)+\(1\dfrac{81}{90}\)
giúp mik với mik cần gấp
= 1,1 + 1,2 + 1,3 + 1,4 + 1,5 + 1,6 + 1,7 + 1,8 + 1,9
= 2,3 + 1,3 + 1,4 + 1,5 + 1,6 + 1,7 + 1,8 + 1,9
= 3,6 + 1,4 + 1,5 + 1,6 + 1,7 + 1,8 + 1,9
= 5 + 1,5 + 1,6 + 1,7 + 1,8 + 1,9
= 6,5 + 1,6 + 1,7 + 1,8 + 1,9
= 8,1 + 1,7 + 1,8 + 1,9
= 9,8 + 1,8 + 1,9
= 11,6 + 1,9
= 13,5
Đúng 0
Bình luận (0)
Tính giá trị biểu thức sau bằng cách thuận tiện nhất và kết quả dưới dạng số thập phân1dfrac{1}{10}+1dfrac{4}{20}+1dfrac{9}{30}+1dfrac{16}{40}+1dfrac{25}{50}+1dfrac{36}{60}+1dfrac{49}{70}+1dfrac{64}{80}+1dfrac{81}{90}
Đọc tiếp
Tính giá trị biểu thức sau bằng cách thuận tiện nhất và kết quả dưới dạng số thập phân
\(1\dfrac{1}{10}\)+\(1\dfrac{4}{20}\)+\(1\dfrac{9}{30}\)+\(1\dfrac{16}{40}\)+\(1\dfrac{25}{50}\)+\(1\dfrac{36}{60}\)+\(1\dfrac{49}{70}\)+\(1\dfrac{64}{80}\)+\(1\dfrac{81}{90}\)
Tính giá trị của biểu thức:
B=\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(B=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(\Rightarrow B=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}\)
\(\Rightarrow B=\dfrac{3}{2.3}-\dfrac{2}{2.3}+\dfrac{4}{3.4}-\dfrac{3}{3.4}+...+\dfrac{10}{9.10}-\dfrac{9}{9.10}\)
\(\Rightarrow B=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(\Rightarrow B=\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
Đúng 0
Bình luận (0)
\(B=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\\ B=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}\\ B=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\\ B=\dfrac{1}{2}-\dfrac{1}{10}\\ B=\dfrac{5}{10}-\dfrac{1}{10}\\ B=\dfrac{4}{10}\\ B=\dfrac{2}{5}\)
Đúng 0
Bình luận (0)
\(B=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(B=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}\)
\(B=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\)
\(B=\dfrac{1}{2}-\dfrac{1}{10}\)
\(B=\dfrac{2}{5}\)
Vậy ...
Đúng 0
Bình luận (0)
Hãy so sánh : \(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+...+\dfrac{1}{9900}\)với \(\dfrac{1}{2}\)
\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{9900}\)
\(=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{2}-\dfrac{1}{100}< \dfrac{1}{2}\)
Vậy...
Đúng 0
Bình luận (0)
\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{9900}\)
\(=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{2}-\dfrac{1}{100}< \dfrac{1}{2}\left(đpcm\right)\)
Vậy...
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức: Q =\((\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{999})\cdot(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6})\)
Cho biểu thức: \(P=\dfrac{1}{x^2-x}+\dfrac{1}{x^2-3x+2}+\dfrac{1}{x^2-5x+6}+\dfrac{1}{x^2-7x+12}+\dfrac{1}{x^2-9x+20}\)
a, Tìm điều kiện của \(x\) để biểu thức P có giá trị
b, Rút gọn biểu thhuwcs P
c, Tính giá trị của P khi \(x\) thỏa mãn: \(x^3-x^2+2=0\)
a: ĐKXĐ: \(x\notin\left\{0;1;2;3;4;5\right\}\)
b: \(P=\dfrac{1}{x^2-x}+\dfrac{1}{x^2-3x+2}+\dfrac{1}{x^2-5x+6}+\dfrac{1}{x^2-7x+12}+\dfrac{1}{x^2-9x+20}\)
\(=\dfrac{1}{x\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(x-3\right)}+\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{1}{\left(x-4\right)\left(x-5\right)}\)
\(=\dfrac{-1}{x}+\dfrac{1}{x-1}-\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-2}+\dfrac{1}{x-3}-\dfrac{1}{x-3}+\dfrac{1}{x-4}-\dfrac{1}{x-4}+\dfrac{1}{x-5}\)
\(=\dfrac{1}{x-5}-\dfrac{1}{x}\)
\(=\dfrac{x-\left(x-5\right)}{x\left(x-5\right)}=\dfrac{5}{x\left(x-5\right)}\)
c: \(x^3-x^2+2=0\)
=>\(x^3+x^2-2x^2+2=0\)
=>\(x^2\cdot\left(x+1\right)-2\left(x-1\right)\left(x+1\right)=0\)
=>\(\left(x+1\right)\left(x^2-2x+2\right)=0\)
=>x+1=0
=>x=-1
Khi x=-1 thì \(P=\dfrac{5}{\left(-1\right)\left(-1-5\right)}=\dfrac{5}{\left(-1\right)\cdot\left(-6\right)}=\dfrac{5}{6}\)
Đúng 1
Bình luận (0)
tính giá trị biểu thức :\(\dfrac{3}{4}\) - \(\dfrac{5}{6}\) x ( \(\dfrac{1}{6}\)+ \(\dfrac{1}{8}\)) : \(\dfrac{7}{12}\)
\(=\dfrac{3}{4}-\dfrac{5}{6}\times\dfrac{7}{24}\times\dfrac{12}{7}=\dfrac{3}{4}-\dfrac{5}{12}=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
\(\dfrac{3}{4}-\dfrac{5}{6}\left(\dfrac{1}{6}+\dfrac{1}{8}\right):\dfrac{7}{12}\)
\(=\dfrac{3}{4}-\dfrac{5}{6}\cdot\dfrac{7}{24}\cdot\dfrac{12}{7}\)
\(=\dfrac{3}{4}-\dfrac{5}{12}\)
\(=\dfrac{4}{12}=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Bài 1. Tính nhanh giá trị của biểu thức sau:
a, E = \(\dfrac{1}{2}\)+ \(\dfrac{1}{3}\)+ \(\dfrac{1}{6}\)+ \(\dfrac{1}{24}\)+ \(\dfrac{1}{8}\)+ \(\dfrac{1}{2}\)+\(\dfrac{1}{12}\)
\(E=\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{8}+\dfrac{1}{2}+\dfrac{1}{12}\)
\(E=\left(\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(\dfrac{1}{3}+\dfrac{1}{6}\right)+\left(\dfrac{1}{8}+\dfrac{1}{12}+\dfrac{1}{24}\right)\)
\(E=\dfrac{2}{2}+\dfrac{3}{6}+\left(\dfrac{1}{8}+\dfrac{3}{24}\right)\)
\(E=1+\dfrac{1}{2}+\left(\dfrac{1}{8}+\dfrac{1}{8}\right)\)
\(E=\left(\dfrac{2}{2}+\dfrac{1}{2}\right)+\dfrac{2}{8}\)
\(E=\dfrac{3}{2}+\dfrac{1}{4}\)
\(E=\dfrac{6}{4}+\dfrac{1}{4}\)
\(E=\dfrac{7}{4}\)
Đúng 1
Bình luận (1)
A=\(\dfrac{1}{2}\)+\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+....+\dfrac{1}{9900}\)
B=\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+....+\dfrac{1}{2009.2011}\)
\(A=\dfrac{1}{2}+\dfrac{3-2}{3.2}+\dfrac{4-3}{3.4}+...+\dfrac{100-99}{100.99}\)
\(A=\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+....+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A=1-\dfrac{1}{100}\)
\(A=\dfrac{99}{100}\)
Đúng 0
Bình luận (0)
\(2B=\dfrac{2}{1.3}+\dfrac{2}{3.5}+....+\dfrac{2}{2007.2009}+\dfrac{2}{2009..2011}\)
\(2B=\dfrac{3-1}{1.3}+\dfrac{5-3}{3,5}+...+\dfrac{2009-2007}{2009.2007}+\dfrac{2011-2009}{2011.2009}\)
\(2B=\dfrac{3}{3}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2007}-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2011}\)
\(2B=1-\dfrac{1}{2011}\)
\(2B=\dfrac{2010}{2011}\)
\(B=\dfrac{2010}{4022}\)
Đúng 0
Bình luận (0)