mọi người giải phương trình này hộ em với à còn phải tìm điều kiện xác định nữa ạ
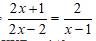
Mọi người giải thích giúp em câu này với được không ạ. Em đã tìm ra được điều kiện xác định là .Nhưng khoảng từ pi/2 đến -pi/4 thì vẫn bao gồm đáp án A mà sao mình lại chọn ạ
TXĐ: `D=RR\\{π/2+kπ ; -π/4 +kπ}`
Mà `-π/2+k2π` và `π/2+k2π \in π/2 +kπ`
`=>` Không nằm trong TXĐ.
giải phương trình và tìm điều kiện xác định giúp mình với ạ!
c: \(\Leftrightarrow x\left(x+3\right)=3+x-3\)
\(\Leftrightarrow x^2+3x-x=0\)
=>x(x+2)=0
=>x=0(loại) hoặc x=-2(nhận)
d: \(\Leftrightarrow\left(x+2\right)\left(x+3\right)+\left(x-2\right)\left(x-3\right)=2x^2+12\)
\(\Leftrightarrow2x^2+12=2x^2+12\)
=>0x=0(luôn đúng)
e: \(\Leftrightarrow x\left(x-3\right)+3\left(x-2\right)=3x-20\)
\(\Leftrightarrow x^2-6-3x+20=0\)
\(\Leftrightarrow x^2-3x+14=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot14=9-56< 0\)
Do đó: Phương trình vô nghiệm
Gợi ý:
ĐKXĐ : Mẫu ≠ 0, từ đó bạn tự xác định
c) Tách \(^{^2x}\)- 3 thành x (x-3) -> quy đồng mẫu-> rút gọn -> tự làm
d) Tách \(^{^2x}\)-9 thành hằng đẳng thức -> như trên
e) Tách \(^{^2x}\)- 5 thành hằng đẳng thức -> như trên
f) Quy đồng mẫu, quá dễ nên không nói thêm
g) Tách \(^{^2x}\)- 1 thành hằng đẳng thức -> như trên
* mọi người giúp mình 2 bài này với ạ*
Bài 8: Cho phương trình (a2 - 4)x -12x + 7 = 0 (a là tham số)
a) Giải phương trình với a = 1
b) Tìm các giá trị của a sao cho phương trình nhận x = 1 là nghiệm.
c) Tìm điều kiện của a để phương trình đã cho luôn có một nghiệm duy nhất
Bài 9: Giải và biện luận phương trình ẩn x theo tham số m
a) (m2 - 9)x - m + 3 = 0
b)\(\dfrac{x+3}{x-1}=\dfrac{x+m}{x+1}\)
Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)

tìm điều kiện xác định và giải phương trình giúp mik vs gấp lắm ạ
b: ĐKXD: x<>1/5; x<>3
PT\(\Leftrightarrow\dfrac{3}{5x-1}-\dfrac{2}{x-3}=\dfrac{-4}{\left(5x-1\right)\left(x-3\right)}\)
=>3x-9-10x+2=-4
=>-7x-7=-4
=>-7x=3
=>x=-3/7
a: ĐKXĐ: x<>2/3; x<>-2/3
\(PT\Leftrightarrow\left(3x+2\right)^2-6\left(3x-2\right)=9x\)
=>9x^2+12x+4-18x+12-9x=0
=>9x^2-15x+16=0
=>\(x\in\varnothing\)
c: ĐKXĐ: x<>1/4; x<>-1/4
PT =>-3(4x+1)=2(4x-1)-6x-8
=>-12x-3=8x-2-6x-8
=>-12x-3=2x-10
=>-14x=-7
=>x=1/2
d: ĐKXĐ: x<>0; x<>2
\(\Leftrightarrow\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8x}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
=>2(5-x)+7(x-2)=4(x-1)+x
=>10-2x+7x-14=4x-4+x
=>5x-4=5x-4
=>0x=0(luôn đung)
Vậy: S=R\{0;2}
e: DKXĐ: x<>0
PT \(\Leftrightarrow\dfrac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{3}{x\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
=>x(x^3+1-x^3+1)=3
=>2x=3
=>x=3/2
tìm điều kiện xác định và giải phương trình giúp mik vs gấp lắm ạ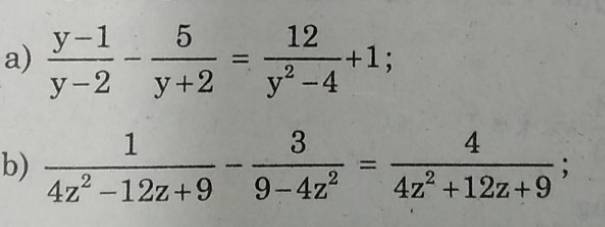
\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(ĐKXĐ:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{5\left(y-2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{\left(y-2\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Leftrightarrow\dfrac{y^2+y-2}{\left(y-2\right)\left(y+2\right)}-\dfrac{5y-10}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{y^2-4}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Leftrightarrow\dfrac{y^2+y-2-5y+10-12-y^2+4}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Rightarrow-4y=0\)
\(\Leftrightarrow y=0\left(tm\right)\)
\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\left(ĐKXĐ:z\ne\pm\dfrac{3}{2}\right)\)
\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}+\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}-\dfrac{4}{\left(2z+3\right)^2}=0\)
\(⇔\dfrac{\left(2z+3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{3\left(2z-3\right)\left(2z+3\right)}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{4\left(2z-3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Leftrightarrow\dfrac{4z^2+12z+9}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{12z^2-27}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{16z^2-48z+36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Leftrightarrow\dfrac{4z^2+12z+9+12z^2-27-16z^2+48z-36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Rightarrow60z-54=0\)
\(\Leftrightarrow60z=54\)
\(\Leftrightarrow z=\dfrac{9}{10}\left(tm\right).\)
\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(dkxd:y\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)-5\left(y-2\right)-12-y^2+4}{y^2-4}=0\)
\(\Leftrightarrow y^2+2y-y-2-5y+10-12-y^2+4=0\)
\(\Leftrightarrow-4y=0\)
\(\Leftrightarrow y=0\left(tmdk\right)\)
Vậy \(S=\left\{0\right\}\)
\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\)
\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}-\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}=\dfrac{4}{\left(2z+3\right)^2}\left(dkxd:z\ne\pm\dfrac{3}{2}\right)\)
\(\Leftrightarrow\left(2z+3\right)^2-3\left(4z^2-9\right)-4\left(2z-3\right)^2=0\)
\(\Leftrightarrow4z^2+12z+9-12z^2+27-4\left(4z^2-12z+9\right)=0\)
\(\Leftrightarrow4z^2+12z+9-12z^2+27-16z^2+48z-36=0\)
\(\Leftrightarrow-24z^2+60z=0\)
\(\Leftrightarrow-12z\left(2z-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-12z=0\\2z-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}z=0\left(tmdk\right)\\z=\dfrac{5}{2}\left(tmdk\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;\dfrac{5}{2}\right\}\)
Cho phương trình: \(x^2-2x+m-3=0\). Tìm giá trị của m để phương trình có hai nghiệm phân biệt x1,x2 thỏa mãn điều kiện: x1\(x^2_1-2x_2+x1.x2=-12\)
Mọi người ơi, giúp em bài này với ạ, em cảm ơn rất nhiều ạ!!!
Lời giải:
Để pt có 2 nghiê pb thì:
$\Delta'=1-(m-3)>0\Leftrightarrow m< 4$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=m-3\end{matrix}\right.\)
Khi đó:
\(x_1^2-2x_2+x_1x_2=-12\)
\(\Leftrightarrow x_1^2-2(2-x_1)+x_1(2-x_1)=-12\)
\(\Leftrightarrow x_1=-2\Leftrightarrow x_2=2-x_1=4\)
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)
Em hãy chọn khẳng định đúng trong hai khẳng định sau đây:
a. Hai phương trình tương đương với nhau thì phải có cùng điều kiện xác định.
b.Hai phương trình có cùng điều kiện xác định có thể không tương đương với nhau.
Mọi người giả hộ em với Em tìm mãi kg ra
Cho phương trình x2+2x+2m=0
a) Tìm m để phương trình có 2 nghiệm trái dấu
b) Tìm m để phương trình có 2 nghiệm x1 , x2 thoả mã điều kiện 2x1+x2=-4
a: Để phương trình có hai nghiệm trái dấu thì 2m<0
hay m<0
b: \(\text{Δ}=2^2-4\cdot2m=-8m+4\)
Để phương trình có hai nghiệm thì -8m+4>=0
=>-8m>=-4
hay m<=1/2
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}2x_1+x_2=-4\\x_1+x_2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-2\\x_2=0\end{matrix}\right.\)
=>2m=0
hay m=0