2) Tìm các số nguyên thỏa mãn: x. (y + 1) + y = 12
DP
Những câu hỏi liên quan
a.Tìm tất cả các số tự nhiên x,y thỏa mãn:
(2.x+1).y=16
b.Tìm tất cả các số nguyên x,y thỏa mãn:
(2.x+1).y=12
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 4. Tìm các số nguyên x và y thỏa mãn (x+1).( y-2) =5 Bài 5. Tìm các số nguyên x và y thỏa mãn xy -2x + 3y
4:
(x+1)(y-2)=5
=>\(\left(x+1;y-2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;7\right);\left(4;3\right);\left(-2;-3\right);\left(-6;1\right)\right\}\)
Đúng 1
Bình luận (0)
Tìm tất cả các cặp số nguyên(x,y)thỏa mãn:2^x+1.3^y=12^x
Ta có : \(2^{x+1}.3^y=12^x\)
\(\Leftrightarrow3^y=\dfrac{12^x}{2^{x+1}}=\dfrac{3^x.4^x}{2^{x+1}}=\dfrac{3^x.2^{2x}}{2^{x+1}}=3^x.2^{2x}:2^{x+1}=3^x.2^{x-1}\)
\(\Leftrightarrow\dfrac{3^y}{3^x}=2^{x-1}\)
\(\Leftrightarrow3^{y-x}=2^{x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}y-x=0\\x-1=0\end{matrix}\right.\Leftrightarrow x=y=1\)(tm)
Vậy (x;y) = (1;1) nghiệm của phương trình trên
Đúng 1
Bình luận (0)
1) Tìm số nguyên tố p để p+2 và p+10 đều nhận giá trị là các số nguyên tố.
2) Tìm cặp số tự nhiên (x ; y) thỏa mãn x ×(y — 1) = 5 × y — 12
Cho các số nguyên x,y thỏa mãn:2x-1.3y+1=12x+y
Tìm x,y
Ta có: 2x-1.3y+1=12x+y
=>2x-1.3y+1=(4.3)x+y
=>2x-1.3y+1=4x+y.3x+y
=>4x+y:2x-1=3y+1:3x+y
=>22x+2y:2x-1=3y+1:3x+y
=>22x+2y-x+1=3y+1-x-y
=>2x+2y+1=31-x
*Xét x+2y+1=0=>2x+2y+1=20=1=31-x=30=>1-x=0=>x=1
=>x+2y+1=0=>1+2y+1=0=>2+2y=0=>2y=-2=>y=-1
*Xét x+2y+1>0=>2x+2y+1 chia hết cho 2=>31-x chia hết cho 2
=>Vô lí
Vậy x=1,y=-1
Đúng 0
Bình luận (0)
neu la so nguyen duong con tim duoc chu tinh so nguyen am thi chiu
Đúng 0
Bình luận (0)
2x-1 . 3y+1 = 12x+y
2x-1 . 3y+1 = 3x+y . 22(x+y)
y + 1 = x + y => x = 1
x - 1 = 2(x + y)
2x + 2y = 1 - 1 = 0
2.1 + 2.y = 0
2 + 2y = 0
2y = -2 => y = -1
Vậy x = 1 ; y = -1
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm các số nguyên x,y thỏa mãn : xy +12=x+y
Lời giải:
$xy+12=x+y$
$\Rightarrow xy-x-y=-12$
$\Rightarrow x(y-1)-y=-12$
$\Rightarrow x(y-1)-(y-1)=-11$
$\Rightarrow (y-1)(x-1)=-11$
Do $x,y$ nguyên nên $x-1,y-1$ cũng nguyên. Ta có bảng: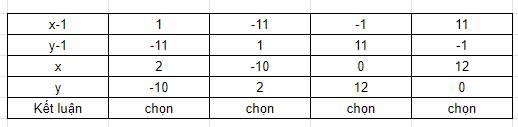
Đúng 4
Bình luận (0)
a) Tìm cặp số x,y nguyên dương thỏa mãn \(x^2+y^2\left(x-y+1\right)-\left(x-1\right)y=22\)
b) Tìm các cặp số x,y,z nguyên dương thỏa mãn \(\dfrac{xy+yz+zx}{x+y+z}=4\)


