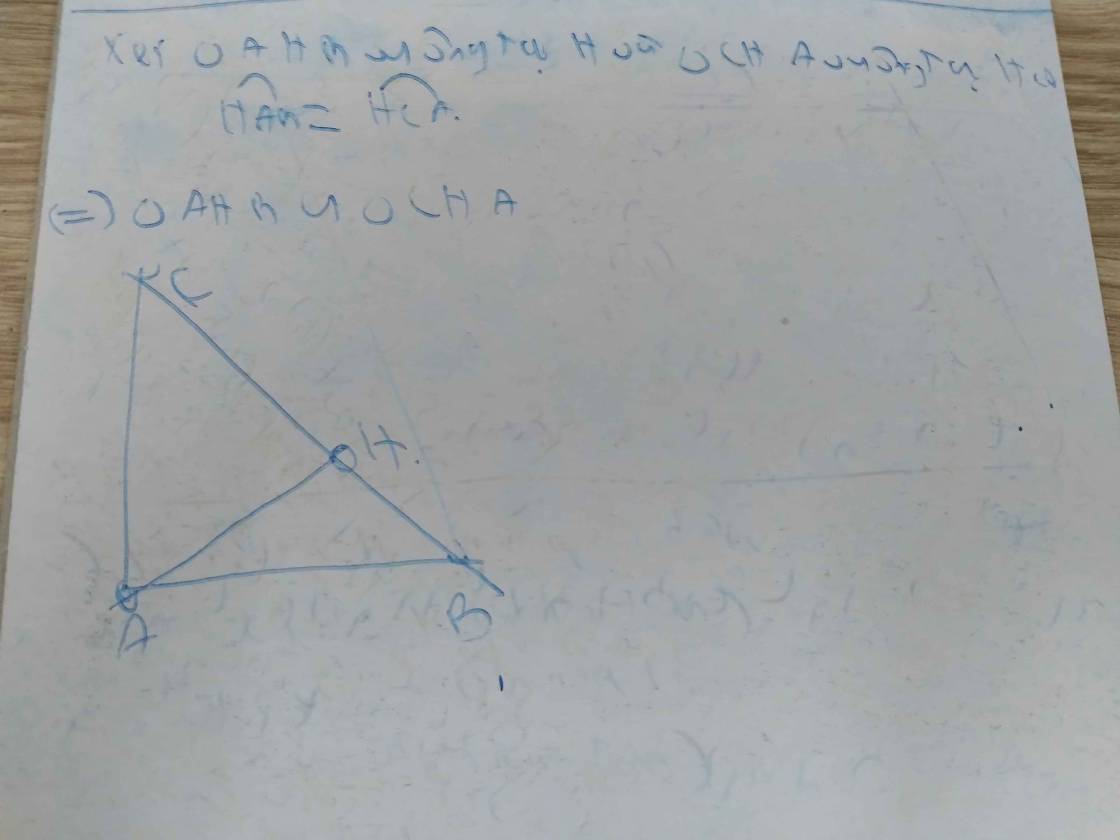
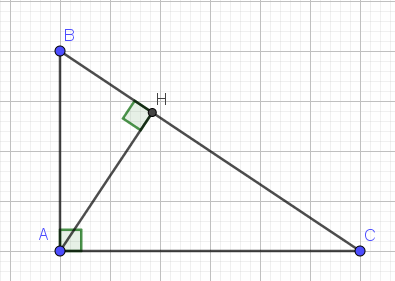
Cho tam giác ABC có AH là đường cao. Chứng minh tam giác AHB đồng dạng với tam giác CHA
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A đường cao AH. Vẽ đường phân giác AD của tam giác CHA , đường phân giác BK của tam giác ABC. Gọi giao của BK và AH, AD lần lượt là E và F. a) chứng minh tam giác AHB đồng dạng với tam giác CHA b) chứng minh tam giác AEF đồng dạng với tam giác BEH c) chứng minh KD //AH d) eh/ad = ed/dc
a: Xét ΔAHB vuông tại H và ΔCHA vuông tạiH có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
c: BK là phân giác
=>AK/CK=BA/BC
ΔAHC có AD là phân giác
nên DH/CD=AH/AC=BA/BC
=>DH/CD=AK/CK
=>KD//AH
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH. Chứng minh tam giác AHB, tam giác CHA đồng dạng ...yêu các bn nhìu nắm lun
xét tam giác AHB và tam giác CHA có:
góc AHB=góc AHC=90độ (gt)
góc B = góc HAC( cùng phụ góc BHA)
do đó : tam giác AHB đồng dạng vs tam giác CHA(g-g)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AH là đường cao.
a) chứng minh tam giác AHB đồng dạng với CHA
b) Kẻ AD là phân giác của tam giác CHA; BK là phân giác của tam giác ABC. BK lần lượt cắt AH, AD tại E và F. Chứng minh tam giác AEF đồng dạng với BEH.
c) KD//AH
d) EH/AB = KD/BC
*giúp mình câu d với ạ!
Thanks.
cho tam giác ABC vuông tại A, đường cao AH
a/ chứng minh tam giác AHB đồng dạng tam giác CBA
b/ kẻ phân giác AD của tam giác CHA và đường phân giác BK của tam giác ABC, BK cắt AH và AD lần lượt tại E và F. Chứng minh tam giác AEF đồng dạng tam giác BEH
c/ KD//AH
d/ chứng minh EH/AB=KD/BC
a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{CBA}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB(g-g)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH , biết AB=15cm , AH=12cm
Chứng minh tam giác AHB đồng dạng với tam giác CHA
Tam giác ABC vuông
=>
BC2 = AB2 + AC2
AH.BC = AB.AC
=>
BC2 = 225 + AC2
12BC = 15AC
Thay BC = 15AC/12 vào pt trên
=>
81AC2 = 32400
=> AC2 = 400
=> AC = 20cm
=> BC = 25cm
BH = \(\sqrt{AB^2-AH^2}\)= \(\sqrt{15^2-12^2}\)= 9
Ta có:
\(\widehat{AHB}\) = \(\widehat{CHA}\)= 90o (1)
cos (\(\widehat{ABH}\)) = \(\frac{BH}{AB}\)= \(\frac{9}{15}\)= \(\frac{3}{5}\)
cos (\(\widehat{CAH}\)) = \(\frac{AH}{AC}\)= \(\frac{12}{20}\)= \(\frac{3}{5}\)
=> \(\widehat{ABH}\)= \(\widehat{CAH}\)(2)
(1), (2) => Tam giác AHB đồng dạng CHA
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ đường phân giác AD của tam giácCHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F.a) Chứng minh: tam giác AHB đồng dạng với tam giác CHA. b) Chứng minh:tam giác AEF đồng dạng tam giác BEH .c) Chứng minh: KD // AH. d) Chứng minh:EH/AB KD/BCGIÚP VỚI !!! ( CHỨNG MINH CHI TIẾT NHÉ )
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ đường phân giác AD của tam giác![]() CHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F.
CHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F.
a) Chứng minh: ![]() tam giác AHB đồng dạng với tam giác CHA.
tam giác AHB đồng dạng với tam giác CHA.
b) Chứng minh:![]() tam giác AEF đồng dạng tam giác BEH .
tam giác AEF đồng dạng tam giác BEH .
c) Chứng minh: KD // AH.
d) Chứng minh:EH/AB = KD/BC
GIÚP VỚI !!! ( CHỨNG MINH CHI TIẾT NHÉ )
Câu 2. Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 15cm AH = 12cm
a) Chứng minh: tam giác AHB đồng dạng tam giác CHA b) Tính độ dài các đoạn BH, CH,ACLời giải:
a. Xét tam giác $AHB$ và $CHA$ có:
$\widehat{AHB}=\widehat{CHA}=90^0$
$\widehat{HAB}=\widehat{HCA}$ (cùng phụ với $\widehat{HAC}$)
$\Rightarrow \triangle AHB\sim \triangle CHA$ (g.g)
b.
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
Từ tam giác đồng dạng phần a suy ra $CH=\frac{AH^2}{BH}=\frac{12^2}{9}=16$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp (O) có đường cao AH, vẽ đường kính AD. Chứng minh tam giác AHB đồng dạng với tam giác ACD.
Mk không biết vẽ hình thông cảm nhé
Ta có AD là đường kính của đường tròn O
\(\Rightarrow\widehat{ACD}=90^0\)
Mặt khác \(\widehat{ADC}=\widehat{ABC}\left(=\frac{1}{2}sđ\widebat{AC}\right)\)
\(\Rightarrow\Delta AHB~\Delta ACD\left(g.g\right)\)
Cho tam giác ABC vuông góc tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. a, Chứng minh AH = MN b, Chứng minh tam giác AHM đồng dạng với tam giác AHB rồi suy ra AH^2 = AM . AB c, Chứng minh tam giác AMN đồng dạng với tam giác ACB d, Cho AB = 6cm, AC = 8cm. Tính diện tích của tam giác AMN.
_____ + H2O --> H2SO4
CuCl2 + NaOH --> NaCl + ____
N2O5 + H2O --> _____
H2 + ___ --> Cu + ___
Fe + ____ --> FeSO4 + H2
BaCl2 + AgNO3 --> _____ + _____
____ + ____ --> Al2O3
CuO + ___ --> Cu + CO2
KMnO4 --> ____ + ____ + _____
Đúng 0
Bình luận (0)