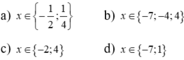a) - 3 =0

<=> (√x-3)(√x+3)-3√x-3=0

<=> (√x-3)(√x+3-3)=0

<=> (√x-3)√x=0

<=> √x-3=0

<=>x=9

b)=x - 3

<=> √(2x -3)² =x-3

<=> 2x-3=x-3

<=>2x-x=-3+3

<=>x=0

c)=3x-1

<=> √(x+3)² =3x-1

<=> x+3=3x-1

<=> -2x=-4

<=>  x=2

Nhớ cho mình 1 tim nha bạn

Lời giải:

a. ĐKXĐ: $x\geq 3$

PT $\Leftrightarrow \sqrt{(x-3)(x+3)}-3\sqrt{x-3}=0$

$\Leftrightarrow \sqrt{x-3}(\sqrt{x+3}-3)=0$

$\Leftrightarrow \sqrt{x-3}=0$ hoặc $\sqrt{x+3}-3=0$

$\Leftrightarrow \sqrt{x-3}=0$ hoặc $\sqrt{x+3}=3$

$\Leftrightarrow x=3$ hoặc $x=6$ (tm)

b.

PT \(\Rightarrow \left\{\begin{matrix} x-3\geq 0\\ 4x^2-12x+9=(x-3)^2=x^2-6x+9\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 3\\ 3x^2-6x=0\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\geq 3\\ 3x(x-2)=0\end{matrix}\right.\)

$\Rightarrow$ không có giá trị $x$ nào thỏa mãn 

Vậy pt vô nghiệm.

c.

PT \(\Rightarrow \left\{\begin{matrix} 3x-1\geq 0\\ x^2+6x+9=(3x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{3}\\ x^2+6x+9=9x^2-6x+1\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{3}\\ 8x^2-12x-8=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{3}\\ 4(x-2)(2x+1)=0\end{matrix}\right.\Leftrightarrow x=2\)

\(a,9\left(2x+1\right)=4\left(x-5\right)^2\)

\(4x^2-40x+100=18x+9\)

\(4x^2-58x+91=0\)

\(\Rightarrow\orbr{\begin{cases}x=\frac{29+3\sqrt{53}}{4}\\x=\frac{29-3\sqrt{53}}{4}\end{cases}}\)

\(b,x^3-4x^2-12x+27=0\)

\(\left(x+3\right)\left(x^2-7x+9\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x+3=0\\x^2-7x+9=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-3\\x=\frac{7\pm\sqrt{13}}{2}\end{cases}}}\)

\(c,x^3+3x^2-6x-8=0\)

\(\left(x+4\right)\left(x-2\right)\left(x+1\right)=0\)

\(Th1:x+4=0\Leftrightarrow x=-4\)

\(Th2:x-2=0\Leftrightarrow x=2\)

\(Th3:x+1=0\Leftrightarrow x=-1\)

\(a,9.\left(2x+1\right)=4.\left(x-5\right)^2\)

\(< =>4x^2-40x+100=18x+9\)

\(< =>4x^2+58x+91=0\)

\(< =>\orbr{\begin{cases}x=\frac{29-3\sqrt{53}}{4}\\x=\frac{29+3\sqrt{53}}{4}\end{cases}}\)

\(b,x^3-4x^2-12x+27=0\)

\(< =>\left(x+3\right)\left(x^2-7x+9\right)=0\)

\(< =>\orbr{\begin{cases}x+3=0\\x^2-7x+9=0\end{cases}}\)

\(< =>\orbr{\begin{cases}x=-3\\x=\frac{7\pm\sqrt{13}}{2}\end{cases}}\)

a). Đặt \(x^2=y\) \(\left(y\ge0\right)\) ta có ;

\(3y^2-12y+9=0\)

\(\Leftrightarrow y^2-4y+3=0\)

Nhận xét : \(a+b+c=1+\left(-4\right)+3=0\)

\(\Rightarrow y_1=1\) (TM \(y\ge0\))

\(y_2=\dfrac{3}{1}=3\)

Với \(y=y_1=1\Rightarrow x^2=1\Leftrightarrow x_1=1;x_2=-1\)

Với \(y=y_2=3\Rightarrow x^2=3\Leftrightarrow x_3=\sqrt{3};x_4=-\sqrt{3}\)

Vậy \(x_1=1;x_2=-1;x_3=\sqrt{3};x_4=-\sqrt{3}\) là các giá trị cần tìm

b) . Đặt \(x^2=y\) \(\left(y\ge0\right)\) ta có ;

\(2y^2+3y-2=0\)

\(\Delta_y=3^2-4\cdot2\cdot\left(-2\right)=9+16=25\) \(\left(\sqrt{\Delta}=5\right)\)

Vì \(\Delta>0\) nên pt có 2 nghiệm phân biệt

\(\Rightarrow\)\(y_1=\dfrac{-3+5}{2\cdot2}=\dfrac{1}{2}\) (TM \(y\ge0\) )

\(y_2=\dfrac{-3-5}{2\cdot2}=-2\) (KTM \(y\ge0\) )

Với \(y=y_1=\dfrac{1}{2}\Rightarrow x^2=\dfrac{1}{2}\Leftrightarrow x_1=\dfrac{1}{4};x_2=-\dfrac{1}{4}\)

Vậy \(x_1=\dfrac{1}{4};x_2=-\dfrac{1}{4}\) là các giá trị cần tìm

c) Đặt \(x^2=y\) \(\left(y\ge0\right)\) ta có ;

\(y^2+5y+1=0\)

\(\Delta_y=5^2-4\cdot1\cdot1=25-4=21\)

Vì \(\Delta>0\) nên pt có 2 nghiệm phân biệt

\(\Rightarrow y_1=\dfrac{-5+\sqrt{21}}{2\cdot1}=\dfrac{-5+\sqrt{21}}{2}\) (KTM \(y\ge0\))

\(y_2=\dfrac{-5-\sqrt{21}}{2\cdot1}=\dfrac{-5-\sqrt{21}}{2}\) (KTM \(y\ge0\))

Vậy pt đã cho vô nghiệm

2: ĐKXĐ: x>=0

\(\sqrt{3x}-2\sqrt{12x}+\dfrac{1}{3}\cdot\sqrt{27x}=-4\)

=>\(\sqrt{3x}-2\cdot2\sqrt{3x}+\dfrac{1}{3}\cdot3\sqrt{3x}=-4\)

=>\(\sqrt{3x}-4\sqrt{3x}+\sqrt{3x}=-4\)

=>\(-2\sqrt{3x}=-4\)

=>\(\sqrt{3x}=2\)

=>3x=4

=>\(x=\dfrac{4}{3}\left(nhận\right)\)

3: 

ĐKXĐ: x>=0

\(3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18}=0\)

=>\(3\sqrt{2x}+5\cdot2\sqrt{2x}-20-3\sqrt{2}=0\)

=>\(13\sqrt{2x}=20+3\sqrt{2}\)

=>\(\sqrt{2x}=\dfrac{20+3\sqrt{2}}{13}\)

=>\(2x=\dfrac{418+120\sqrt{2}}{169}\)

=>\(x=\dfrac{209+60\sqrt{2}}{169}\left(nhận\right)\)

4: ĐKXĐ: x>=-1

\(\sqrt{16x+16}-\sqrt{9x+9}=1\)

=>\(4\sqrt{x+1}-3\sqrt{x+1}=1\)

=>\(\sqrt{x+1}=1\)

=>x+1=1

=>x=0(nhận)

5: ĐKXĐ: x<=1/3

\(\sqrt{4\left(1-3x\right)}+\sqrt{9\left(1-3x\right)}=10\)

=>\(2\sqrt{1-3x}+3\sqrt{1-3x}=10\)

=>\(5\sqrt{1-3x}=10\)

=>\(\sqrt{1-3x}=2\)

=>1-3x=4

=>3x=1-4=-3

=>x=-3/3=-1(nhận)

6: ĐKXĐ: x>=3

\(\dfrac{2}{3}\sqrt{x-3}+\dfrac{1}{6}\sqrt{x-3}-\sqrt{x-3}=-\dfrac{2}{3}\)

=>\(\sqrt{x-3}\cdot\left(\dfrac{2}{3}+\dfrac{1}{6}-1\right)=-\dfrac{2}{3}\)

=>\(\sqrt{x-3}\cdot\dfrac{-1}{6}=-\dfrac{2}{3}\)

=>\(\sqrt{x-3}=\dfrac{2}{3}:\dfrac{1}{6}=\dfrac{2}{3}\cdot6=\dfrac{12}{3}=4\)

=>x-3=16

=>x=19(nhận)

a.\(2\sqrt{12x}-3\sqrt{3x}+4\sqrt{48x}=17\)

=>\(4\sqrt{3x}-3\sqrt{3x}+16\sqrt{3x}=17\)

=>\(17\sqrt{3x}=17\)

=>\(\sqrt{3x}=1\)

=>\(x=\dfrac{1}{3}\)

b.Ta có:\(\sqrt{x^2-6x+9}=1\)

=>\(\sqrt{\left(x-3\right)^2}=1\)

=>\(\left|x-3\right|=1\)

Vậy có hai trường hợp:

TH1:\(x-3=1\)

=>\(x=4\)

TH2:\(x-3=-1\)

=>\(x=2\)

a) ĐKXĐ: \(x\ge0\)

Ta có: \(2\sqrt{12x}-3\sqrt{3x}+4\sqrt{48x}=17\)

\(\Leftrightarrow2\cdot2\cdot\sqrt{3x}-3\cdot\sqrt{3x}+4\cdot4\cdot\sqrt{3x}=17\)

\(\Leftrightarrow4\sqrt{3x}-3\sqrt{3x}+16\sqrt{3x}=17\)

\(\Leftrightarrow17\sqrt{3x}=17\)

\(\Leftrightarrow\sqrt{3x}=1\)

\(\Leftrightarrow3x=1\)

hay \(x=\dfrac{1}{3}\)(nhận)

Vậy: \(S=\left\{\dfrac{1}{3}\right\}\)

b) ĐKXĐ: \(x\in R\)

Ta có: \(\sqrt{x^2-6x+9}=1\)

\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=1\)

\(\Leftrightarrow\left|x-3\right|=1\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=1\\x-3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)

Vậy: S={2;4}