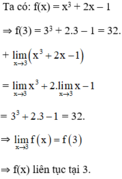f(x) = 2x + 3 tại x0 = 1
SP
Những câu hỏi liên quan
F(x) = \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\left(x\ne1\right)\\3x+m\left(x=1\right)\end{matrix}\right.\)
Tại x0=1. Tìm m để hàm số liên tục tại x0=1
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x^2+2\right)}{x-1}=\lim\limits_{x\rightarrow1}\left(x^2+2\right)=3\)
\(f\left(1\right)=3.1+m=m+3\)
Hàm số liên tục tại \(x_0=1\) khi và chỉ khi \(\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\)
\(\Rightarrow m+3=3\Rightarrow m=0\)
Đúng 3
Bình luận (0)
Dùng định nghĩa xét tính liên tục của hàm số f ( x ) = x 3 + 2 x - 1 tại x 0 = 3 .
tính đạo hàm y=f(x)=x2+2x-1 tại x0=1
tính giá trị của hàm số
a) y= f(x)= x2 +x-2 tại x0 =\(\dfrac{1}{2}\)
b)y=f(x)=\(\dfrac{2\sqrt{3}}{x^2+1}\) tại x0 =\(\sqrt{3}\)
a: \(f\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^2+\dfrac{1}{2}-2=\dfrac{1}{4}+\dfrac{1}{2}-2=\dfrac{3}{8}-2=\dfrac{3-16}{8}=-\dfrac{13}{8}\)
b: \(f\left(\sqrt{3}\right)=\dfrac{2\sqrt{3}}{\left(\sqrt{3}\right)^2+1}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\)
Đúng 1
Bình luận (0)
Xét ba mệnh đề sau: (1) Nếu hàm số f(x) có đạo hàm tại điểm
x
x
0
thì f(x) liên tục tại điểm đó. (2) Nếu hàm số f(x) liên tục tại điểm
x
x
0
thì f(x) có đạo hàm tại điểm đó. (3) Nếu f(x) gián đoạn tại
x
x
0
thì chắc chắn f(x) không có đạo hàm tại điểm đó. Trong ba câu trên: A. Có hai câu đúng và một câ...
Đọc tiếp
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Đáp án A
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f (x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f ( x ) = x ta có D= R nên hàm số f(x) liên tục trên R.
Nhưng ta có l i m x → 0 + f ( x ) - f ( 0 ) x - 0 = l i m x → 0 + x - 0 x - 0 = l i m x → 0 + x - 0 x - 0 = 1 l i m x → 0 - f ( x ) - f ( 0 ) x - 0 = l i m x → 0 - x - 0 x - 0 = l i m x → 0 - - x - 0 x - 0 = - 1
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.
Đúng 0
Bình luận (0)
Xét ba mệnh đề sau:(1) Nếu hàm số f(x) có đạo hàm tại điểm
x
x
0
thì f(x) liên tục tại điểm đó.(2) Nếu hàm số f(x) liên tục tại điểm
x
x
0
thì f(x) có đạo hàm tại điểm đó.(3) Nếu f(x) gián đoạn tại
x
x
0
thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: A. Có hai câu đúng và một câu sai. ...
Đọc tiếp
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
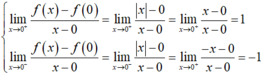
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Đúng 0
Bình luận (0)
Xét ba mệnh đề sau:(1) Nếu hàm số f(x) có đạo hàm tại điểm
x
x
0
thì f(x) liên tục tại điểm đó.(2) Nếu hàm số f(x) liên tục tại điểm
x
x
0
thì f(x) có đạo hàm tại điểm đó.(3) Nếu f(x) gián đoạn tại
x
x
0
thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: A. Có hai câu đúng và một câu sai....
Đọc tiếp
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
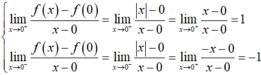
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Đúng 0
Bình luận (0)
Xét ba mệnh đề sau:(1) Nếu hàm số f(x) có đạo hàm tại điểm
x
x
0
thì f(x) liên tục tại điểm đó.(2) Nếu hàm số f(x) liên tục tại điểm
x
x
0
thì f(x) có đạo hàm tại điểm đó.(3) Nếu f(x) gián đoạn tại
x
x
0
thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: A. Có hai câu đúng và một câu sai....
Đọc tiếp
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai .
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó. Đây là mệnh đề sai.
- Ví dụ: Lấy hàm f(x) = |x| ta có tập xác định D = R . +)Với mọi
x
0
≠ 0 thì 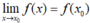
+)Lại có:
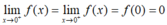
→ Nên hàm số f(x) liên tục trên R.
+) Nhưng ta có:
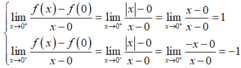
→ Nên hàm số không có đạo hàm tại x = 0.
→ Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vì (1) là mệnh đề đúng nên ta suy ra : Nếu f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Đúng 0
Bình luận (0)
tính đạo hàm : y=f(x)=\(x^2+2x-1\)tại x0=1