cho tam giác ABCcó đường trung tuyến AM và trong tâm G . khi đó tỉ sốGM/GA bằng:
A.1/3
B.2/3
C.1/2
D.2
6H
Những câu hỏi liên quan
cho tam giác ABC coa đường trung tuyến AM và trọng tâm G . khi đó tỉ soo GM/AG bằng :
A, 1/3
B,2/3
C,1/2
D,2
cho tam giác ABC coa đường trung tuyến AM và trọng tâm G . khi đó tỉ soo GM/AG bằng :
A, 1/3
B,2/3
C,1/2
D,2
Đúng 0
Bình luận (0)
Theo định lý trọng tâm của đường trung tuyến:
`-` Trọng tâm của tam giác cách đỉnh `2/3,` cách đáy `1/3`
Vì `G` là trọng tâm của tam giác `ABC -> AG=2/3 AM, GM=1/3 AM`
`->` Tỉ số của \(\dfrac{GM}{AG}=\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{2}{3}\right)}=\dfrac{1}{2}\)
`-> C`
Đúng 2
Bình luận (0)
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó
G
A
→
A.
2
G
M
→
B.
2
3
G
M
→
C.
-...
Đọc tiếp
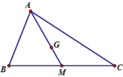
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó G A → =
A. 2 G M →
B. 2 3 G M →
C. - 2 3 A M →
D. 1 2 A M →
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó
G
A
→
Đọc tiếp
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó G A → =
Chọn C.
Ta có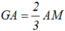 
.Mặt khác 
và 
ngược hướng =>
.
Đúng 0
Bình luận (0)
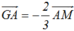Bài 1 :Cho tam giác ABC có hai đường trung tuyến BE và CF cắt nhau tại G.Chứng minh G là trọng tâm của tam giác ABC.(Gợi ý trọng tâm là điểm chung của ba đường trung tuyến nên trọng tâm là điểm chung của...)
Bài 2 Cho tam giác ABC có đường trung tuyến AD và trọng tâm G.Đã biết GA=2/3 AD,hãy chứng minh GA=2GD,AD=3GD.
Cho tam giác ABC vuông tại A, có AM là đường trung tuyến. Trên tia đối của tia MA, lấy hai điểm D và K sao cho MA=MK và GA=GD ( G là trọng tâm của tam giác ABC)
a) C/m AM=1/2 BC. Tính độ dài đoạn GA,GM biết rằng AB= 6cm, AC=8cm
b) C/m BD=GC
a) Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{1}{2}BC\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
Đúng 0
Bình luận (0)
Bài 1 Cho tam giác ABC có hai đường trung tuyến BE và CF cắt nhau tại G.Chứng minh G là trọng tâm của tam giác ABC.(GỢI Ý Trọng tâm là điểm chung của ba đường trung tuyến nên trọng tâm là điểm chung của ...)
BÀI 2 Cho tam giác ABC có đường trung tuyến AD VÀ trọng tâm G.Đã biết GA=2/3 AD.hãy chứng minh GA=2GD,AD=3GD.
HELP ME,GIÚP M VỚI MÌNH SẼ LIKE ,MÌNH ĐANG CẦN RẤT GẤP
hông biết
cho ΔABC có trung tuyến AM., G là trọng tâm tam giác. Khẳng định đúng là
A. GA=GB=GC
B. GA=\(\dfrac{2}{3}\)GM
C. GA=GM
D. GA=\(\dfrac{2}{3}\)AM
Vì `G` là trọng tâm của tam giác
`@` Theo tính chất của trọng tâm (cách đỉnh `2/3,` cách đáy `1/3`)
`-> GA = 2GM, GA= 2/3 AM`
Xét các đáp án trên `-> D.`
Đúng 2
Bình luận (0)
Cho tam giác ABC ,AM là đường trung tuyến có độ dài 6cm và G là trọng tâm của tam giác ABC .Tính độ dài đoạn thẳng GA
Theo tính chất của trọng tâm thì ta có :
\(AG=\frac{2}{3}AM\)
Mà AM = 6cm
\(\Rightarrow AG=\frac{2}{3}.6=4\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Khi đó
A.\(AM = 2GM\). B.\(AM = 2AG\). C.\(GA = 3GM\). D.\(GA = 2GM\).
