tam giác ABC có trực tâm H(1;1) và phương trình cạnh AB: 5x-2y+6=0, phương trình cạnh AC: 4x +7y -21=0. Viết phương trình cạnh BC. Giải chi tiết dùm mình pls và ▲ là t...g...
H24
Những câu hỏi liên quan
Cho tam giác ABC có ba góc nhọn và H là trực tâm. Tìm ảnh của tam giác ABC qua phép vị tự tâm H, tỉ số 1/2.
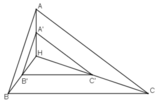
+ ΔABC nhọn ⇒ trực tâm H nằm trong ΔABC.
+ Gọi A’ = V(H; ½) (A)
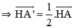
⇒ A’ là trung điểm AH.
+ Tương tự :
B’ = V(H; ½) (B) là trung điểm BH.
C’ = V(H; ½) (C) là trung điểm CH.
⇒ V(H; ½)(ΔABC) = ΔA’B’C’ với A’; B’; C’ là trung điểm AH; BH; CH.
Đúng 0
Bình luận (0)
Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.
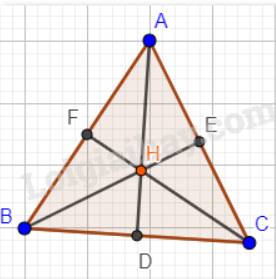
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.
Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD;
\(AD \bot BC; BE \bot AC; CF \bot AB\)
Xét tam giác ADB và tam giác ADC có:
AD chung
\(\widehat{ADB}=\widehat{ADC} (=90^0)\)
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).
Tương tự, ta cũng được, AC = BC
Xét tam giác ABC có AB = AC = BC nên là tam giác đều.
Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.
Đúng 0
Bình luận (0)
Trong mp xOy cho tam giác ABC. bt A(3;-1) B(-1;2) I(1;-1) là trọng tâm của tam giác ABC. Trực tâm H của tam giác ABC có tọa độ (a;b). Tính a+3b
Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4). Tìm tọa độ trực tâm H của tam giác ABC?
A. H( 1;1)
B. H( 1; 2)
C. (2;1)
D. (2;2)
Chọn D.
Gọi H (x; y) là trực tâm tam giác ABC nên
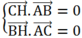
Mà
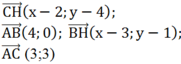
Suy ra:
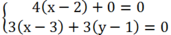
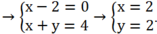
Vậy H(2; 2).
Đúng 0
Bình luận (0)
Cho tam giác ABC có A( -1; 3) ; B( -2; 0) và C( 5;1). Trực tâm H của tam giác ABC có toạ độ là:
A. (3 ; -1)
B. (-1 ; 3)
C. (2 ; -1)
D. (2 ; -3)
Ta có:
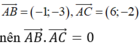
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(-1; 1); trực tâm H(-31; 41) và tâm đường tròn ngoại tiếp tam giác ABC là I(16; 18). Tìm tọa độ các đỉnh B; C
Cho tam giác ABC có A(3;1) B(2,6) C(4;-1) a.Tính chứ vi tam giác ABC B.Tính góc A C.Tìm toạ độ trực tâm H của tam giác ABC.
a: A(3;1); B(2;6); C(4;-1)
\(AB=\sqrt{\left(2-3\right)^2+\left(6-1\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)
\(AC=\sqrt{\left(4-3\right)^2+\left(-1-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)
\(BC=\sqrt{\left(4-2\right)^2+\left(-1-6\right)^2}=\sqrt{2^2+7^2}=\sqrt{53}\)
Chu vi tam giác ABC là:
\(C_{ABC}=\sqrt{26}+\sqrt{5}+\sqrt{53}\left(đvđd\right)\)
b: Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+5-53}{2\cdot\sqrt{26\cdot5}}\simeq-0,96\)
=>\(\widehat{A}\simeq165^0\)
c: Gọi H(x,y) là trực tâm của ΔABC
\(\overrightarrow{AH}=\left(x-3;y-1\right)\)
\(\overrightarrow{BH}=\left(x-2;y-6\right)\)
\(\overrightarrow{BC}=\left(2;-7\right);\overrightarrow{AC}=\left(1;-2\right)\)
H là trực tâm nên ta có: AH\(\perp\)BC và BH\(\perp\)AC
=>\(\left\{{}\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\\overrightarrow{BH}\cdot\overrightarrow{AC}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left(x-3\right)+\left(-7\right)\left(y-1\right)=0\\1\left(x-2\right)+\left(-2\right)\left(y-6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-6-7y+7=0\\x-2-2y+12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-7y=-1\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-7y=-1\\2x-4y=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-1+20=19\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{19}{3}\\x=-10+2y=-10-\dfrac{38}{3}=-\dfrac{68}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:
a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;
b) Nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
a)
Ta có:
G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);
H là trực tâm của tam giác ABC (giao điểm của ba đường cao);
I là giao điểm của ba đường phân giác của tam giác ABC;
O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).
Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.
Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.
b)
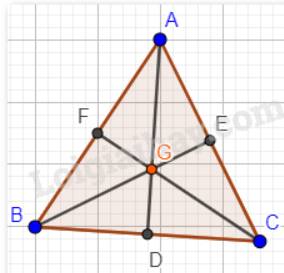
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).
Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Tham khảo:
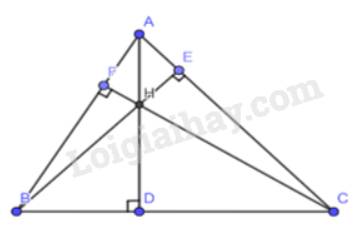
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.
Đúng 0
Bình luận (0)




