1: Xét ΔOPQ có 

I là trung điểm của PQ

IN//OP

Do đó: N là trung điểm của OQ

Xét ΔOPQ có 

I là trung điểm của PQ

IM//OQ

Do đó: M là trung điểm của OP

Xét ΔMPI và ΔNQI có 

MP=NQ

\(\widehat{P}=\widehat{Q}\)

PI=QI

Do đó: ΔMPI=ΔNQI

Suy ra: IM=IN

hay ΔIMN cân tại I

2: Ta có: OM=ON

nên O nằm trên đường trung trực của MN(1)

Ta có: IM=IN

nên I nằm trên đường trung trực của MN(2)

Từ (1) và (2) suy ra OI là đường trung trực của MN

Hehj

a: Xét ΔABC có

H,O lần lượt là trung điểm của CB,CA

=>HO là đường trung bình của ΔABC

=>HO//AB và \(HO=\dfrac{AB}{2}\)

b: Ta có: HO//AB

O\(\in\)HD

Do đó: HD//AB

Ta có: HO=AB/2

HO=HD/2

Do đó: AB=HD

Xét tứ giác ABHD có

HD//AB

HD=AB

Do đó: ABHD là hình bình hành

=>AH cắt BD tại trung điểm của mỗi đường

mà I là trung điểm của AH

nên I là trung điểm của BD

=>B,I,D thẳng hàng

a: Xét tứ giác ADCE có

O là trung điểm chung của AC và DE

góc ADC=90 độ

Do đó: ADCE là hình chữ nhật

b: Xét tứ giác AEDB có

AE//DB

AE=DB

Do đó: AEDB là hình bình hành

c:BD=CD=BC/2=6cm

AO=OD=10/2=5cm

AD=8cm

P=(5+5+8)/2=18/2=9cm

\(S=\sqrt{9\cdot\left(9-8\right)\left(9-5\right)\left(9-5\right)}=\sqrt{9\cdot1\cdot4\cdot4}=3\cdot2\cdot2=12\left(cm^2\right)\)

a: Xét tứ giác ADCE có

O là trung điểm chung của AC và DE

góc ADC=90 độ

Do đó: ADCE là hình chữ nhật

b: Xét tứ giác AEDB có

AE//DB

AE=DB

Do đó: AEDB là hình bình hành

c:BD=CD=BC/2=6cm

AO=OD=10/2=5cm

AD=8cm

P=(5+5+8)/2=18/2=9cm

\(S=\sqrt{9\cdot\left(9-8\right)\left(9-5\right)\left(9-5\right)}=\sqrt{9\cdot1\cdot4\cdot4}=3\cdot2\cdot2=12\left(cm^2\right)\)

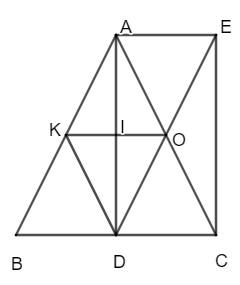
a) Tứ giác ADCE có: O là trung điểm của AC, O là trung điểm của BD

nên tứ giác ADCE là hình bình hành

Có \(\widehat{ADC}=90^\circ\)

Vậy tứ giác ADCE là hình chữ nhật.

b) AECD là hình chữ nhật \(\Rightarrow AE=DC\), AE // DC

Tam giác ABC cân tại A có AD là đường cao

\(\Rightarrow\) AD là đường trung tuyến của tam giác ABC

\(\Rightarrow\) D là trung điểm của BC \(\Rightarrow BD=DC=\dfrac{1}{2}BC\)

Xét tứ giác AEDB có: \(AE=BD\), AE // BD

Vậy tứ giác AEBD là hình bình hành.

c) Tam giác ADC vuông tại D: \(AC^2=AD^2+DC^2\) (Định lí Pi-ta-go)

\(AD=\sqrt{AC^2-DC^2}=\sqrt{10^2-6^2}=8\) (cm)

\(S_{OAD}=\dfrac{1}{2}S_{ADC}=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot8\cdot6=12\) (cm²).

d) Tam giác ADC có: O là trung điểm của AC, I là trung điểm của AD

nên OI là đường trung bình của tam giác ADC

\(\Rightarrow\) OI // BC.

Tam giác ABC có: OK // BC, O là trung điểm của AC

\(\Rightarrow\) K là trung điểm của AB.

Tam giác ABC: O là trung điểm của AC, K là trung điểm của AB

nên OK là đường trung bình của tam giác ABC

\(\Rightarrow OK=\dfrac{1}{2}BC\)

Xét tứ giác KOCD: OK = DC, OK // DC

nên tứ giác KOCD là hình bình hành

\(\Rightarrow\) KD = OC

\(\Rightarrow KD=\dfrac{1}{2}AC\)

\(AE=DC=\dfrac{1}{2}BC\)

Để AE = DK thì AC = BC

Tam giác ABC có AC = AB = BC nên tam giác ABC đều

Vậy tam giác ABC đều thì AE = DK.