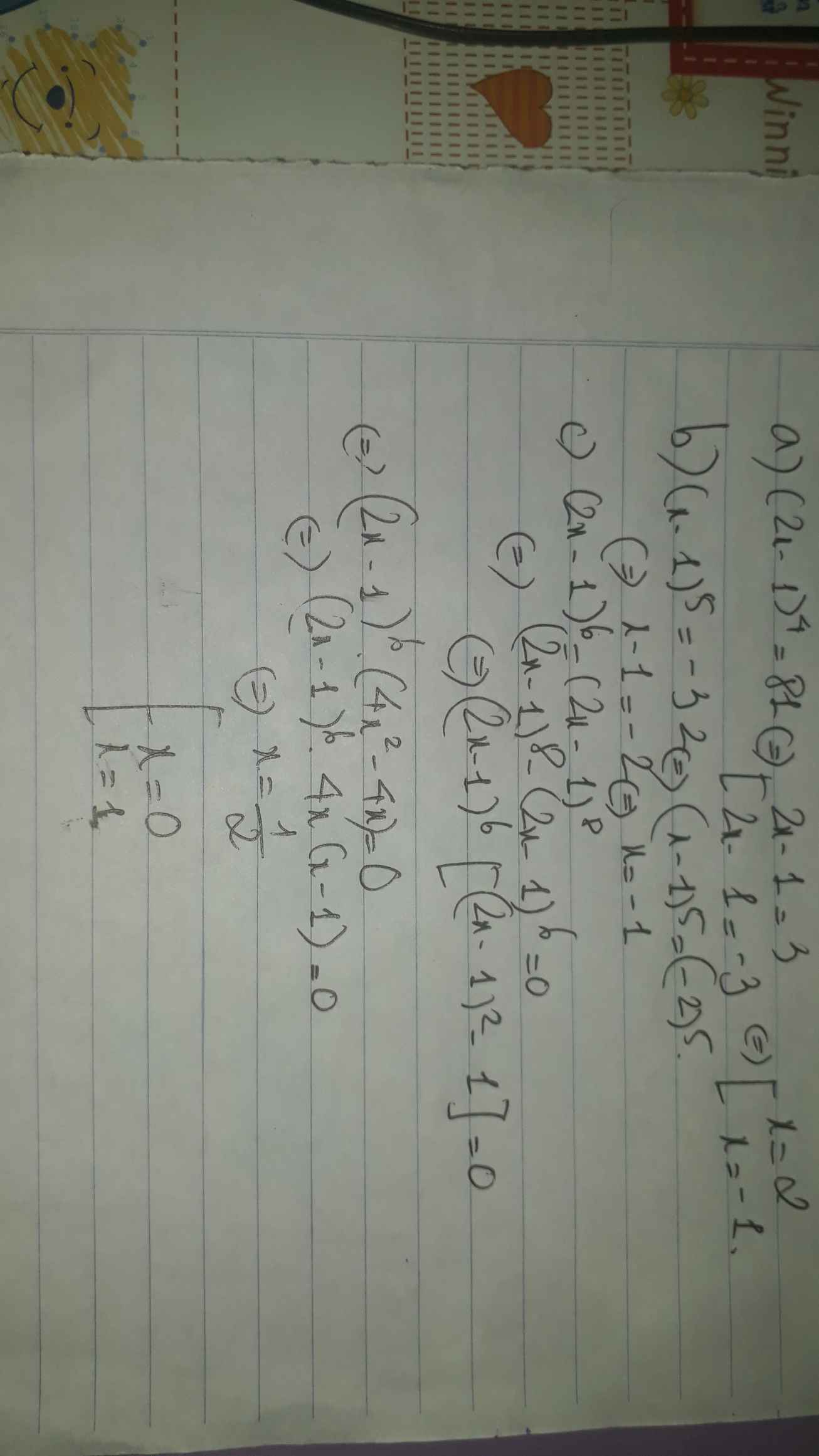Tìm các số tự nhiên x,yx,y biết rằng: (2x+1)(2x+2)(2x+3)(2x+4) − 5y = 11879
MN
Những câu hỏi liên quan
Tìm các số tự nhiên x, y biết rằng: (2x + 1) . (2x + 2) . (2x + 3) . (2x + 4) - 5y = 11879
(2x + 1) . (2x + 2) . (2x + 3) . (2x + 4) - 5y = 11879
[(2x + 1). (2x + 4)].[(2x + 2) . (2x + 3)] -5y = 11879
(4x2+10x+4).(4x2+10x+6) -5y = 11879
Đặt t= 4x2+10x+4
t(t+2) -5y = 11879
t2+2t-5y = 11879
(t+1)2 = 11880+5y
(4x2+10x+5)2 = 5(2376+y)
=> x = 0; y=-2371
Đúng 0
Bình luận (0)
giải chi tiết cho mình từ chỗ thứ 8 đi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các số tự nhiên x, y biết rằng: (2x 1) . (2x 2) . (2x 3) . (2x 4) - 5y = 11879
Bài 1: Tìm số hữu tỉ x biết:a, ( 2x - 1 )4 81 b, ( x - 1 )5 -32 c, ( 2x - 1 )6 ( 2x - 1 )8Bài 2: Tìm các số tự nhiên x, y biết rằng: a, 2x + 1 . 3y 12x. b, 10x : 5y 20y c, 2x 4y - 1 và 27y 3x + 8
Đọc tiếp
Bài 1: Tìm số hữu tỉ x biết:
a, ( 2x - 1 )4 = 81 b, ( x - 1 )5 = -32
c, ( 2x - 1 )6 = ( 2x - 1 )8
Bài 2: Tìm các số tự nhiên x, y biết rằng:
a, 2x + 1 . 3y = 12x. b, 10x : 5y = 20y
c, 2x = 4y - 1 và 27y = 3x + 8
Bài 2:
a: Ta có: \(2^{x+1}\cdot3^y=12^x\)
\(\Leftrightarrow2^{x+1}\cdot3^y=2^{2x}\cdot3^x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=2x\\x=y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a) Tìm số tự nhiên x, y biết: (2x+1)(y-3)=12
b) Tìm số tự nhiên x biết: 2x+2x+1+2x+2+...+2x+2015=22019-8
c) So sánh: 3625 và 2536
a,(2x+1)(y-3)=12
⇒⇒2x+1 và y-3 ∈∈Ư(12)={±1;±2;±3;±4;±6;±12}{±1;±2;±3;±4;±6;±12}
| 2x+1 | 1 | -1 | 2 | -2 | 3 | -3 |
| y-3 | 12 | -12 | 6 | -6 | 4 | -4 |
| x | 0 | -1 | 1212 | −32−32 | 1 | -2 |
| y | 15 | -9 | 9 | 3 | 7 | -1 |
=>x=0,y=15
Đúng 0
Bình luận (0)
c) Ta có: \(36^{25}=\left(6^2\right)^{25}=6^{50}\)
\(25^{36}=\left(5^2\right)^{36}=5^{72}\)
Ta có: \(6^{50}=\left(6^5\right)^{10}=7776^{10}\)
mà \(5^{70}=\left(5^7\right)^{10}=78125^{10}\)
nên \(6^{50}< 5^{70}\)
mà \(5^{70}< 5^{72}\)
nên \(6^{50}< 5^{72}\)
hay \(36^{25}< 25^{36}\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
a) Tìm số tự nhiên x, y biết: (2x+1)(y-3)=12
b) Tìm số tự nhiên x biết: 2x+2x+1+2x+2+...+2x+2015=22019-8
c) So sánh: 3625 và 2536
a) Tìm số tự nhiên x, y biết: (2x+1)(y-3)=12
b) Tìm số tự nhiên x biết: 2x+2x+1+2x+2+...+2x+2015=22019-8
c) So sánh: 3625 và 2536
a/
Với $x,y$ là số tự nhiên $2x+1, y-3$ là số nguyên. Mà $(2x+1)(y-3)=12$ nên $2x+1$ là ước của 12.
$2x+1>0, 2x+1$ lẻ nên $2x+1\in \left\{1;3\right\}$
Nếu $2x+1=1\Rightarrow y-3=12$
$\Rightarrow x=0; y=15$
Nếu $2x+1=3\Rightarrow y-3=4$
$\Rightarrow x=1; y=7$
Vậy...........
Đúng 1
Bình luận (0)
b/
$2^x+2^{x+1}+2^{x+2}+...+2^{x+2015}=2^{2019}-8$
$2^x(1+2+2^2+2^3+...+2^{2015})=2^{2019}-8(1)$
$2^x(2+2^2+2^3+2^4+...+2^{2016})=2^{2020}-16(2)$ (nhân 2 vế với 2)
Lấy (2) trừ (1) theo vế thì:
$2^x(2^{2016}-1)=2^{2020}-2^{2019}-8$
$2^x(2^{2016}-1)=2^{2019}(2-1)-8=2^{2019}-8$
$2^x(2^{2016}-1)=2^3(2^{2016}-1)$
$\Rightarrow 2^x=2^3$
$\Rightarrow x=3$
Đúng 1
Bình luận (0)
c/
$25^{36}=(5^2)^{36}=5^{72}$
$36^{25}=(6^2)^{25}=6^{50}=(6^5)^{10}< (5^7)^{10}=5^{70}< 5^{72}$
$\Rightarrow 25^{36}> 36^{25}$
Đúng 0
Bình luận (0)
Tìm các số tự nhiên x, y biết:
a, ( 8 . 2x ) ( 11 - 5y )
b, x - 3 = y ( x - 1 )
Câu a đề bài thiếu
b, \(x-3=y\left(x-1\right)\)
\(\frac{x-1-2}{x-1}=y\)
\(1-\frac{2}{x-1}=y\)
\(\frac{2}{x-1}=1-y\)
Có \(1-y\in Z\)
\(\Rightarrow\frac{2}{x-1}\in Z\)
\(\Rightarrow x-1\inƯ\left(2\right)\)
Tính các trường hợp của x rồi thay vào tàm y và tìm những cặp thỏa mãn điều kiện
tìm các số tự nhiên x,y biết rằng: (2x + 1)(2x + 2)(2x + 3)(2x + 4)(2x + 5) - 5y = 11879
Đặt A=(2x+1)(2x+2)(2x+3)(2x+4)
Ta có: 2x⋅Alà tích của 5 số tự nhiên liên tiếp nên 2x⋅A⋮5
Nhưng 2x⋮̸ 5, do đó A⋮5
Nếu y≥1y≥1, ta có (2x+1)(2x+2)(2x+3)(2x+4)−5y⋮5
Mà 11879⋮̸ 5⇒y≥1 không thỏa mãn suy ra y=0
Khi đó pt⇔(2x+1)(2x+2)(2x+3)(2x+4)−1=11879
⇔(2x+1)(2x+2)(2x+3)(2x+4)=11880
⇔(2x+1)(2x+2)(2x+3)(2x+4)=9⋅10⋅11⋅12⇔x=3
Vậy {x=3
y=0 là 2 số tự nhiên cần tìm
a,Tìm số tự nhiên x biết: 3^2x+3-3^2x+1=216
b. Tìm tất cả các số tự nhiên x và y thoả mãn 2x.(y+1)+y=6