Giải dùm em hệ phương trình này với ạ!
em cảm ơn
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
 mọi người lập bảng giải hộ em bằng hệ phương trình với ạ. E cần gấp, em cảm ơn
mọi người lập bảng giải hộ em bằng hệ phương trình với ạ. E cần gấp, em cảm ơn
Ai giải dùm em bài này em cảm ơn ạ!

giúp em với ạ, em cảm ơn. đây là giải hệ phương trình
a. 4x + 5y=9
2x-y=1
\(\left\{{}\begin{matrix}4x+5y=9\\2x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=9\\10x-5y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14x=14\\4x+5y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\4.1+5y=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Giải giúp em phương trình này ạ em cảm ơn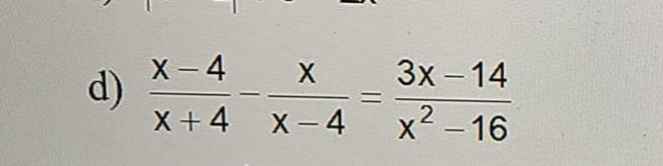
`[x-4]/[x+4]-x/[x-4]=[3x-14]/[x^2-16]` `ĐK: x \ne +-4`
`<=>[(x-4)^2-x(x+4)]/[(x-4)(x+4)]=[3x-14]/[(x-4)(x+4)]`
`=>x^2-8x+16-x^2-4x=3x-14`
`<=>3x+8x+4x=16+14`
`<=>15x=30`
`<=>x=2` (t/m)
Vậy `S={2}`
`(x - 4)/(x + 4) - x/(x - 4) = (3x - 14)/(x^2 - 16)`
`=>` `x = 2`
Giải phương trình: 2cos4x.cos2x - 2cos4x.sin2x=0 Giúp em câu này với ạ, cảm ơn!!
\(\Leftrightarrow2cos4x\left(cos2x-sin2x\right)=0\)
\(\Leftrightarrow cos4x=0\) (do \(cos4x=cos^22x-sin^22x\) đã bao hàm \(cos2x-sin2x\))
\(\Rightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)
mọi người ơi giải giúp em phương trình này với ạ
3x(2-x)-5 = 1-(3x ngũ 2 + 2)
giải chi tiết giúp em với ạ cảm ơn mọi người nhiều ạ
3x(2-x)-5=1-(3x2+2)
<=>6x-3x2-5=-3x2-2
<=>6x=3
<=>x=1/2
giải dùm em cái này vs ạ
em cảm ơn mọi người nhiều
Giải giúp em cái điều kiện của phương trình này với ạ...
I 8-X I = x2 + x đk : .................
Em cảm ơn các a.c.e trước ạ! ![]()
để \(\left|8-x\right|=8-x< =>8-x\ge0< =>x\le8\)
\(=>8-x=x^2+x< =>x^2+2x-8=0\)
\(< =>\left(x+1\right)^2-3^2=0< =>\left(x-2\right)\left(x+4\right)=0\)
\(=>\left[{}\begin{matrix}x=2\left(TM\right)\\x=-4\left(TM\right)\end{matrix}\right.\)
*để\(\left|8-x\right|=x-8< =>8-x< 0< =>x>8\)
\(=>x-8=x^2+x< =>x^2=-8\)(vô lí)
vậy x=2 hoặc x=-4