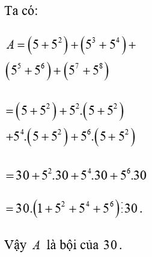cho biểu thức: M = 5 + 52 + 53 + .........+ 580. chứng tỏ rằng M chia hết cho 30
YA
Những câu hỏi liên quan
Cho biểu thức: M 5 + 52 + 53 + … + 580. Chứng tỏ rằng M chia hết cho 30.
Đọc tiếp
Cho biểu thức: M = 5 + 52 + 53 + … + 580. Chứng tỏ rằng M chia hết cho 30.
M=(5+5^2)+5^2(5+5^2)+...+5^78(5+5^2)
=30(1+5^2+...+5^78) chia hết cho 30
Đúng 0
Bình luận (0)
Cho biểu thức: M = 5 + 52 + 53 + … + 580. Chứng tỏ rằng:
a) M chia hết cho 6.
b) M không phải là số chính phương.
a) M = \(5+5^2+5^3+...+5^{80}\)
\(\Leftrightarrow M=5.\left(1+5\right)+5^3\left(1+5\right)+...+5^{79}\left(1+5\right)\)
\(\Leftrightarrow M=5.6+5^3.6+...+5^{79}.6\)
\(\Leftrightarrow M=6.\left(5+5^3+...+5^{79}\right)⋮6\)
=> M chi hết cho 6 => điều phải chứng minh
Đúng 5
Bình luận (2)
) M = (5+5^2) + (5^3+5^4) + … + (5^79+5^80)
M = 5(1+5) + 5^3(1+5) + … + 5^79(1+5)
M= 5.6 + 5^3.6 + … + 5^79.6
M = 6(5+5^3+…+5^79) chia hết cho 6
b) Ta thấy : M = 5 + 52+ 53+ ... + 580 cchia hết cho số nguyên tố 5
Mặt khác, do: 52 + 53 + ... 580 chia hết cho 52 (vì tất cả các số hạng đều chia hết cho 52)
=> M = 5 + 52 + 53 + ... + 580 không chia hết cho 52 (do 5 không chia hết cho 52)
=> M chia hết cho 5 nhưng không chia hết cho 52
=> M không phải số chính phương
Đúng 4
Bình luận (3)
Cho biểu thức: M = 5 + 52 + 53 + ... + 580. Chứng tỏ rằng:
a. M chia hết cho 6
b. M không phải là số chính phương
c. Tìm x ∈ N sao cho 5x = 4.A + 5
Mình chỉ cần câu b và câu c thôi nhé !
Help me !!!Pleaseeeeeeeeeeeeeeeeeeee !
Bày cho nè ! Bài tập đội Tuyển đúng ko
1.Câu a cậu làm được rồi chứ gì ?
b, Vì 6 chia hết cho 6 =) 6. ( 5 +53+...+580)chia hết cho 6
Nên M chia hết cho 6=)M là hợp số
Vậy M ko phải là số chính phương
c, M=5+52+53+...+580
5M=5.(5+52+53+...+580)
5M=52+53+...+580+581
5M-M=(52+53+...+580+581) - (5+52+53+...+580)
4M=52-53-...-580-581 - 5-52-53-...-580
4M=(52-52)+(53-53) +...+(580 -580)+581-5
4M=581-5
4M+5=581-5+5
4M+5=581
=)5x=4M+5
=)581=4M+5
Vậy x=81
Đáp số =...
HOK TOT
Đúng 0
Bình luận (2)
Chứng tỏ rằng: Giá trị của biểu thức
A
5
+
5
2
+
5
3
+
.
.
.
+
5
8
là bội của 30
Đọc tiếp
Chứng tỏ rằng: Giá trị của biểu thức A = 5 + 5 2 + 5 3 + . . . + 5 8 là bội của 30
Ta có: A = 5 + 5 2 + 5 3 + 5 4 + 5 5 + 5 6 + 5 7 + 5 8
= 5 + 5 2 + 5 2 5 + 5 2 + 5 4 5 + 5 2 + 5 6 5 + 5 2
= 30 + 5 2 . 30 + 5 4 . 30 + 5 6 . 30
= 30 . ( 1 + 5 2 + 5 4 + 5 6 ) ⋮ 30
Vậy A là bội của 30
Đúng 2
Bình luận (0)
Chứng tỏ rằng: Giá trị của biểu thức A = 5 + 5 2 + 5 3 + . . . . + 5 8 là bội của 30.
Cho B= 5+52+53+...589 +590. Chứng tỏ rằng B chia hết cho 31
\(B=5+5^2+5^3+...+5^{88}+5^{89}+5^{90}\)
\(=\left(5+5^2+5^3\right)+\left(5^4+5^5+5^6\right)+...+\left(5^{88}+5^{89}+5^{90}\right)\)
\(=5\left(1+5+5^2\right)+5^4\left(1+5+5^2\right)+...+5^{88}\left(1+5+5^2\right)\)
\(=31\left(5+5^4+...+5^{88}\right)⋮31\)
Đúng 1
Bình luận (1)
Chứng tỏ rằng 1+ 5 + 52 + 53 +... + 5402 + 5403 + 5404 chia hết cho 31
Đặt \(A=1+5+5^2+5^3+...+5^{402}+5^{403}+5^{404}\)
\(\Rightarrow A=\left(1+5+5^2\right)+\left(5^3+5^4+5^5\right)+...+\left(5^{399}+5^{400}+5^{401}\right)+\left(5^{402}+5^{403}+5^{404}\right)\)
\(\Rightarrow A=31.1+31.5^3+...+31.5^{402}\)
\(\Rightarrow A=31\left(1+5^3+5^6+...+5^{402}\right)\)
\(\Rightarrow A⋮31\left(đpcm\right)\)
Đúng 1
Bình luận (1)
Chứng tỏ rằng:
1+5+52+53+......+5402+5403+4404
chia hết cho 31?
\(\left(1+5+5^2\right)+\left(5^3+5^4+5^5\right)+...+\left(5^{402}+5^{403}+5^{404}\right)\\ =31+5^3.\left(1+5+5^2\right)+...+5^{402}.\left(1+5+5^2\right)\\ =31+5^3.31+...+5^{402}.31\\ =31.\left(1+5^3+...+5^{402}\right)⋮31\left(DPCM\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng C = 5 + 5 2 + 5 3 + ... + 5 8 chia hết cho 30
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: C = 5 + 5 2 + 5 3 + ... + 5 8 = 5 + 5 2 + 5 3 + 5 4 + 5 5 + 5 6 + 5 7 + 5 8 = 30 + 5 2 5 + 5 2 + 5 4 5 + 5 2 + 5 6 5 + 5 2 = 30 + 5 2 5 + 5 2 + 5 4 5 + 5 2 + 5 6 5 + 5 2 = 30 + 5 2 .30 + 5 4 .30 + 5 6 .30 = 30. 1 + 5 2 + 5 4 + 5 6 Áp dụng tính chất chia hết của một tích ta có: 30 ⋮ 30 ⇒ 30. 1 + 5 2 + 5 4 + 5 6 ⋮ 30 ⇒ C = 30. 1 + 5 2 + 5 4 + 5 6 ⋮ 30 |
Đúng 1
Bình luận (0)