Giúp em bài 1 và bài 2 ạ
ND
Những câu hỏi liên quan
mong mn giúp em bài 1 và bài 2 ạ
Bài 1:
a) Ta có: \(2x-3=4x+6\)
\(\Leftrightarrow2x-4x=6+3\)
\(\Leftrightarrow-2x=9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy: \(S=\left\{-\dfrac{9}{2}\right\}\)
Đúng 1
Bình luận (0)
Bài 1:
b) Ta có: \(\dfrac{x+2}{4}-x+3-\dfrac{1-x}{8}=0\)
\(\Leftrightarrow\dfrac{2\left(x+2\right)}{8}+\dfrac{8\left(-x+3\right)}{8}+\dfrac{x-1}{8}=0\)
Suy ra: \(2x+4-8x-24+x-1=0\)
\(\Leftrightarrow-5x-21=0\)
\(\Leftrightarrow-5x=21\)
hay \(x=-\dfrac{21}{5}\)
Vậy: \(S=\left\{-\dfrac{21}{5}\right\}\)
Đúng 1
Bình luận (0)
Bài 1: bạn tự kết luận nghiệm nhé, vì đây là những phương trình cơ bản nên mình giải tắt chút
a, \(2x-3=4x+6\Leftrightarrow-2x=9\Leftrightarrow x=-\dfrac{9}{2}\)
b, \(\dfrac{x+2}{4}+3-\dfrac{1-x}{8}=0\)
\(\Leftrightarrow\dfrac{2x+4+24-1+x}{8}=0\Rightarrow3x+27=0\Leftrightarrow x=-3\)
c, \(x\left(x-1\right)+x\left(x+3\right)=0\Leftrightarrow x^2-x+x^2+3x=0\)
\(\Leftrightarrow2x^2+2x=0\Leftrightarrow2x\left(x+1\right)=0\Leftrightarrow x=0;x=-1\)
d, \(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)ĐK : \(x\ne-1;3\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x^2+x-x^2+3x}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x+1\right)\left(x-3\right)}\Rightarrow0=0\)
Vậy phương trình có vô số nghiệm
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp em bài 1 và 2 với bài nào cũng được ạ
Câu 2:
a: Ta có: \(25x^2-9=0\)
\(\Leftrightarrow\left(5x-3\right)\left(5x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-\dfrac{3}{5}\end{matrix}\right.\)
b: Ta có: \(\left(x-4\right)^2-\left(x-2\right)\left(x+2\right)=6\)
\(\Leftrightarrow x^2-8x+16-x^2+4=6\)
\(\Leftrightarrow-8x=-14\)
hay \(x=\dfrac{7}{4}\)
c: Ta có: \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x-7\right)\left(x+7\right)=0\)
\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5\left(x^2-49\right)=0\)
\(\Leftrightarrow5x^2+2x+10-5x^2+245=0\)
\(\Leftrightarrow x=-\dfrac{255}{2}\)
Đúng 0
Bình luận (1)
GIÚP EM Ý D,E BÀI 1 VÀ BÀI 2 VỚI Ạ
d: \(\Leftrightarrow x^2-x-1=x+2\)
\(\Leftrightarrow x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
e: \(\Leftrightarrow x^2-x-2+x-1=3x+4\)
\(\Leftrightarrow x^2-3-3x-4=0\)
\(\Leftrightarrow x^2-3x-7=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-7\right)=37\)
Vì Δ>0 nên pt có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{37}}{2}\\x_2=\dfrac{3+\sqrt{37}}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (1)
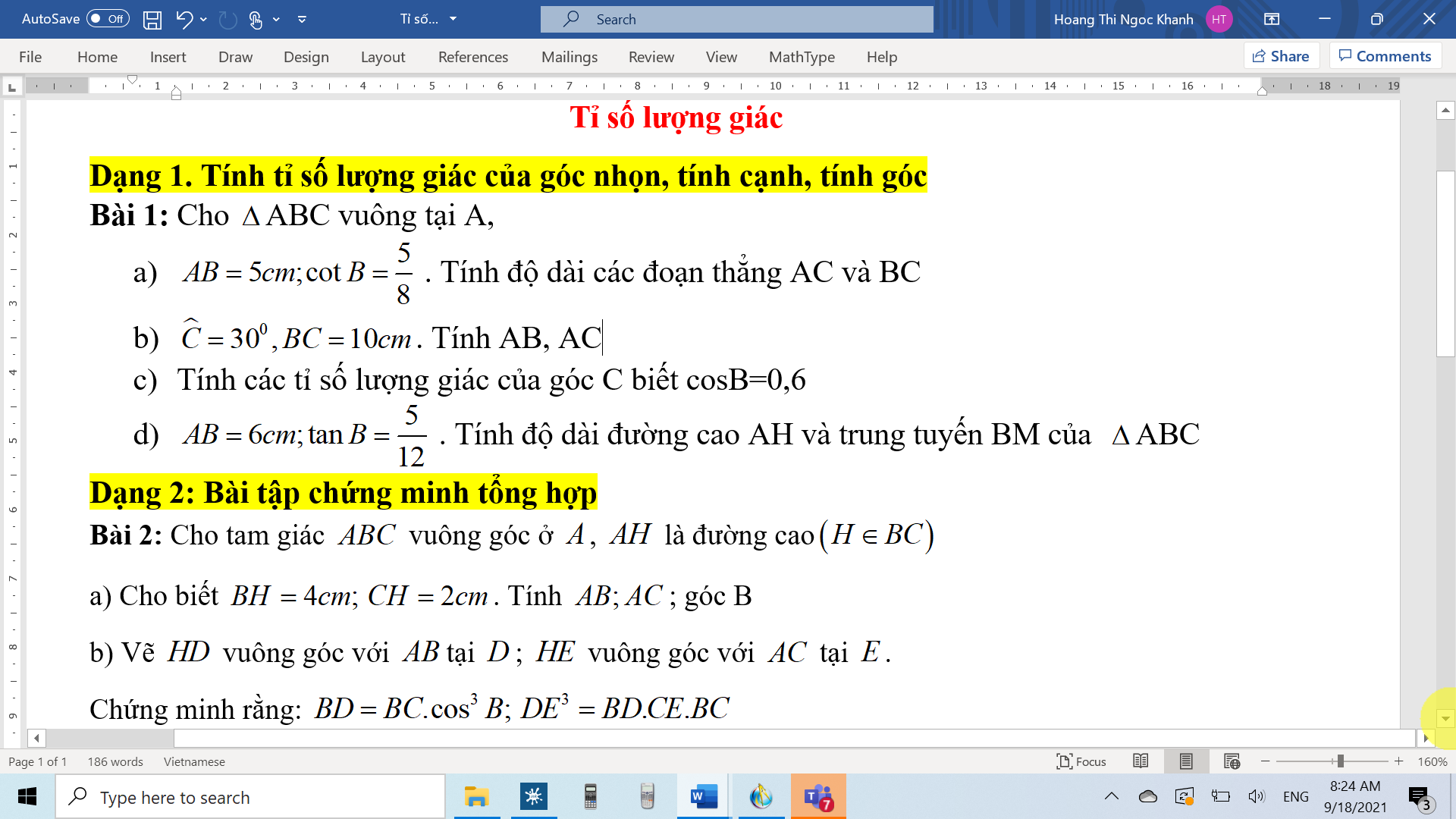
giúp em câu b bài 1 và ý 2 câu b bài 2 ạ
Thầy cô giúp em ý2 bài 1 và ý3 bài 2 với ạ, em không biết làm 
1.2
Đề câu này bị lỗi đoạn cuối, chỗ nằm giữa \(-3x+...+2014\) là gì ấy nhỉ? \(2^2\) đúng không?
Đây là giải theo cách dịch đề bài:
\(A=5x^5-15x^4+14x^3-12x^2-3x+2^2+2014\)
Khi đó:
\(x=\sqrt[3]{2}+1\Rightarrow x-1=\sqrt[3]{2}\)
\(\Rightarrow\left(x-1\right)^3=2\)
\(\Rightarrow x^3-3x^2+3x-1=2\)
\(\Rightarrow x^3-3x^2+3x-3=0\)
Ta có:
\(A=5x^2\left(x^3-3x^2+3x-3\right)-x^3+3x^2-3x+4+2014\)
\(=5x^2.0-\left(x^3-3x^2+3x-3\right)+2015\)
\(=-0+2015=2015\)
Còn nếu đề bài là:
\(A=\left(5x^5-15x^4+14x^3-12x^2-3x+2\right)^2+2014\)
Thì kết quả là: \(A=1+2014=2015\)
Đúng 2
Bình luận (0)
2.3
Lại 1 câu đề lỗi nữa, biểu thức của pt là:
\(x^2+\left(2m-2\right)x-m^2=0\)
hay \(x^2+2m-2x-m^2=0\)?
Người đánh đề bài này rất ẩu tả, vô trách nhiệm
Coi như đề bài là: \(x^2+\left(2m-2\right)x-m^2=0\)
Ta có:
\(\Delta'=\left(m-1\right)^2+m^2=\dfrac{1}{2}\left(2m-1\right)^2+\dfrac{1}{2}>0\) ; \(\forall m\)
Pt luôn có 2 nghiệm với mọi m
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-m^2\end{matrix}\right.\)
\(\left|x_1-x_2\right|=6\Leftrightarrow\left(x_1-x_2\right)^2=36\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=36\)
\(\Leftrightarrow\left(2m-2\right)^2+4m^2=36\)
\(\Leftrightarrow m^2-m-4=0\Rightarrow m=\dfrac{1\pm\sqrt{17}}{2}\)
Đúng 1
Bình luận (0)
Giúp em bài 1 và 2 ạ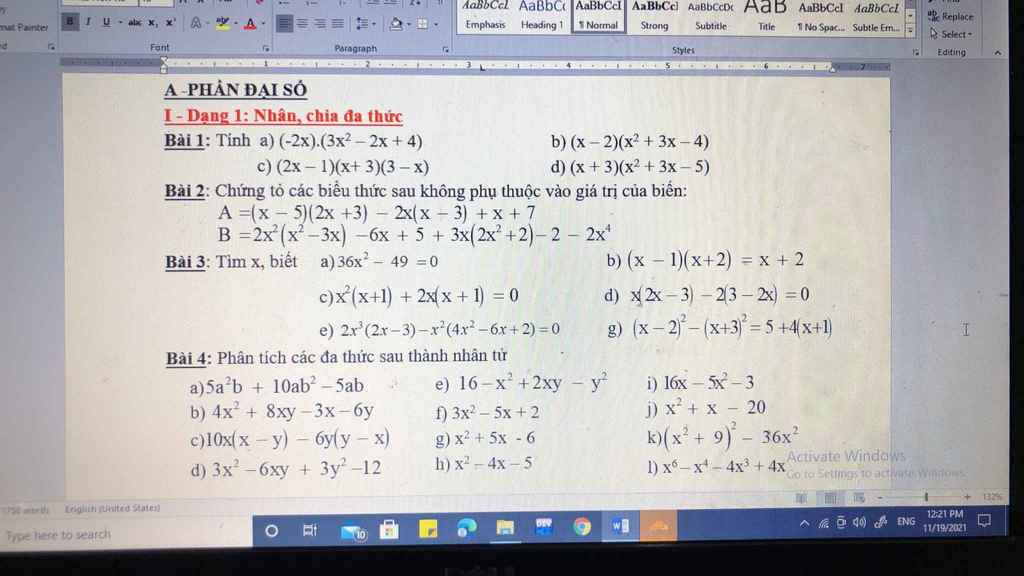
Bài 1:
\(a,\left(-2x\right)\left(3x^2-2x+4\right)=-6x^3+4x^2-8x\\ b,\left(x-2\right)\left(x^2+3x-4\right)=x\left(x^2+3x-4\right)-2\left(x^2+3x-4\right)=x^3+3x^2-4x-2x^2-6x+8=x^3+x^2-10x+8\)
\(c,\left(2x-1\right)\left(x+3\right)\left(3-x\right)=\left(2x-1\right)\left(9-x^2\right)=9\left(2x-1\right)-x^2\left(2x-1\right)=18x-9-2x^3+x^2\\ d,\left(x+3\right)\left(x^2+3x-5\right)=x\left(x^2+3x-5\right)+3\left(x^2+3x-5\right)=x^3+3x^2-5x+3x^2+9x-15=x^3+6x^2+4x-15\)
Bài 2:
\(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\\ =2x^2-10x+3x-15-2x^2+6x+x+7\\ =-8\)
\(B=2x^2\left(x^2-3x\right)-6x+5+3x\left(2x^2+2\right)-2-2x^4\\ =2x^4-6x^3-6x+5+6x^3+6x-2-2x^4\\ =3\)
Vậy A,B không phụ thuộc vào giá trị của biến
Đúng 1
Bình luận (0)

giúp em bài 1 và 2 đi ạ
1.
\(a,\) Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=18\left(cm\right)\\AH=\sqrt{18\left(50-18\right)}=24\left(cm\right)\end{matrix}\right.\)
\(b,\cos\widehat{ABC}=\dfrac{AB}{BC}=\dfrac{3}{5}\approx\cos53^0\Leftrightarrow\widehat{ABC}\approx53^0\)
Mà BH là đường cao \(\left(BH\perp AI\right)\) và là trung tuyến \(\left(AH=IH\right)\) nên tg ABI cân tại B
Do đó BH cũng là p/g
Vậy \(2\widehat{ABC}=\widehat{ABI}=2\cdot53^0=106^0\)
Đúng 2
Bình luận (0)
Bài 2:
a: Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay AC=20(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=12\left(cm\right)\\BH=9\left(cm\right)\\CH=16\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải chi tiết phần b bài 1 và phần b bài 2 giúp em với ạ
Bài 2:
b: Ta có: \(B=\dfrac{15-5\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{-5\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-2}=1\)
Đúng 1
Bình luận (0)
Thầy cô giúp em bài 2 ý 1 và 3 với ạ, em đang cần gấp ạ 
3) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m^2-6\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-6\right)\)
\(=4m^2-8m+4-4m^2+24\)
\(=-8m+28\)
Để phương trình có hai nghiệm phân biệt x1;x2 thì Δ>0
\(\Leftrightarrow-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{1}=2m-2\\x_1x_2=m^2-6\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-6\right)-16=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+12-16=0\)
\(\Leftrightarrow2m^2-8m=0\)
\(\Leftrightarrow2m\left(m-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=4\left(loại\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)





