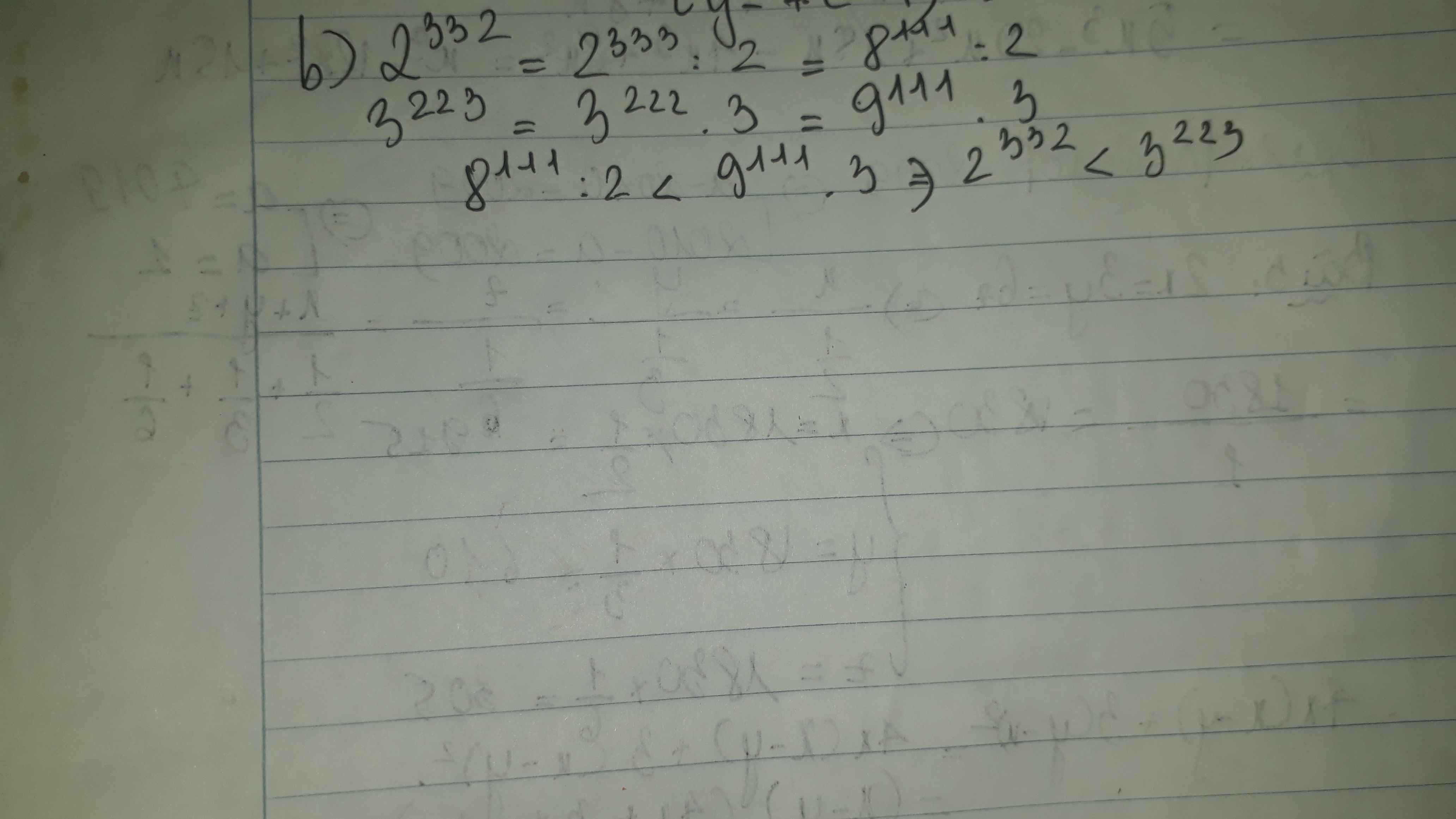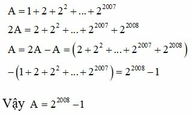Tính: M=22010-(22009+22008+22007+...+21+20).
PA
Những câu hỏi liên quan
Tính: M = 22010 - (22009 + 22008 + ... + 21 + 20)
Đặt A = 22009 + 22008 + ... + 21 + 20. Khi đó, M = 22010 - A
Ta có 2A = 22010 + 22009 + ... + 22 + 21.
Suy ra 2A - A = 22010 - 20 = 22010 - 1.
Do đó M = 22010 - A = 22010 - (22010 - 1) = 22010 - 22010 + 1 = = 1.
Đúng 0
Bình luận (0)
M=2^2010-(2^2009+2^2008+2^2007+...+2^1+2^0)
M=22010-22009-22008-22007-...-21-20
=>2M=22011-22010-22009-22008-...-22-21
=>2M-M=22011-22010-22009-22008-...-22-21-(22010-22009-22008-22007-...-21-20)
=>M=22011-22010-22009-22008-...-22-21-22010+22009+22008+22007+...+21+20
=22011-22010-22010+20
=22011-2.22010+1
=22011-22011+1
=1
vậy M=1
a) Tính M = 22010 - ( 22009 + 22008 + ..... + 21 + 20 )
b) So sánh: 2332 và 3223
Giúp vs
Bài 1. Tìm x biết
a) (x+3)3=640000
b) 275.3x=910
c) (1/33.9).3x=27
d) 85.4x=221
Bài 2. Tính
M=22010-(22009+22008+...+21+20)
Cho A = 1 + 2 + 2 2 + . . . + 2 2007 . Chứng minh: A = 2 2008 - 1
Cho
A
1
+
2
+
2
2
+
.
.
.
+
2
2007
. Chứng minh:
A
2
2008...
Đọc tiếp
Cho A = 1 + 2 + 2 2 + . . . + 2 2007 . Chứng minh: A = 2 2008 - 1
A = 1 + 2 + 2 2 + . . . + 2 2007
2 A = 2 + 2 2 + . . . + 2 2007 + 2 2008
A = 2A - A = ( 2 + 2 2 + . . . + 2 2007 + 2 2008 ) - ( 1 + 2 + 2 2 + . . . + 2 2007 ) = 2 2008 - 1
Vậy A = 2 2008 - 1
Đúng 0
Bình luận (0)
B=1+2+22+23+...+22008/1-22009
Đặt A=1+2+22+...+220081+2+22+...+22008
=>2A=2.(1+2+22+...+220081+2+22+...+22008)
=>2A=2+22+23+...+220092+22+23+...+22009
=>2A-A=(2+22+23+...+220092+22+23+...+22009)-(1+2+22+...+220081+2+22+...+22008)
=>A=22009−122009−1
=>A=(-1).(−2)2009(−2)2009+(-1).1
=>A=(-1).[(−2)2009+1][(−2)2009+1]
=>A=(-1).(1−22009)(1−22009)
=>1+2+22+...+220081+2+22+...+22008/1-2200922009
=
Đúng 0
Bình luận (0)
Giải:
Đặt A=1+2+22+23+...+22008
2A=2+22+23+24+...+22009
2A-A=(1+2+22+23+...+22008)-(2+22+23+24+...+22009)
A =1-22009
Vậy B=1-22009/1-22009=1
Chúc bạn học tốt!
Đúng 0
Bình luận (1)
Cho A = 1 + 2 + 2 2 + . . . + 2 2009 + 2 2010 . Tìm số dư khi chia A cho 7
Ta có: A = 1 + 2 + 2 2 + . . . + 2 2009 + 2 2010
= 1 + 2 ( 1 + 2 + 2 2 ) + ... + 2 2008 ( 1 + 2 + 2 2 )
= 1 + 2 ( 1 + 2 + 4 ) + ... + 22008 ( 1 + 2 + 4 )
= 1 + 2 . 7 + ... + 2 2008 . 7 = 1 + 7 ( 2 + ... + 2 2008 )
Mà 7 ( 2 + ... + 2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.
Đúng 0
Bình luận (0)
Cho A = 1 + 2 + 2 2 + ... + 2 2009 + 2 2010 . Tìm số dư khi chia A cho 7.
Ta có: A = 1 + 2 + 2 2 + 2 3 + ... + 2 2008 + 2 2009 + 2 2010
= 1 + 2 ( 1 + 2 + 22 ) + ... + 2 2008 ( 1 + 2 + 22 )
= 1 + 2 ( 1 + 2 + 4 ) + ... + 2 2008 ( 1 + 2 + 4 )
= 1 + 2 . 7 + ... + 2 2008 . 7 = 1 + 7 ( 2 + ... + 2 2008 )
Mà 7 ( 2 + ... + 2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.
Đúng 0
Bình luận (0)
Cho A = 1+21+22+233+...+22007
a)Tính 3A
b)Chứng minh : A = 22008--1
A \(=\)\(1+2^1+2^2+...+2^{2007}\)
⇒2 A \(=\)\(2+2^2+...+2^{2007}+2^{2008}\)
2A - A \(=\)( \(2+2^2+...+2^{2007}+2^{2008}\) ) - ( \(1+2^1+2^2+...+2^{2007}\) )
A\(=\)\(2^{2008}-1\)
\(3A=3\left(2^{2008}-1\right)\)
\(=3.2^{2008}-3\)
Đúng 0
Bình luận (0)
bài 1 so sánh A và B biết : a) A=20+21+22+ 23+......+22010
b) B=22011-1
A = 2⁰ + 2¹ + 2² + 2³ + ... + 2²⁰¹⁰
⇒ 2A = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰¹¹
⇒ A = 2A - A = (2 + 2² + 2³ + 2⁴ + ... + 2²⁰¹¹) - (2⁰ + 2¹ + 2² + 2³ + ... + 2²⁰¹⁰)
= 2²⁰¹¹ - 2⁰
= 2²⁰¹¹ - 1
= B
Vậy A = B
Đúng 1
Bình luận (0)