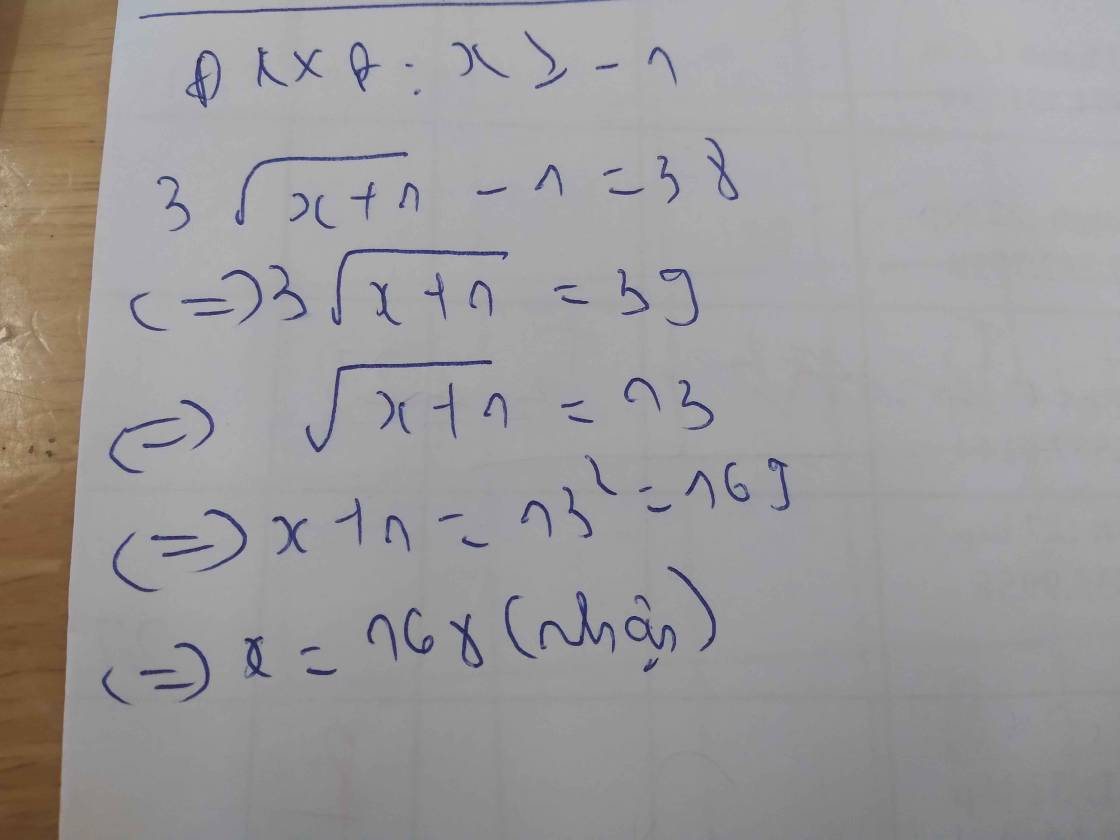Vũ Minh Tuấn, Băng Băng 2k6, Hoàng Tử Hà, đề bài khó wá, Lê Gia Bảo, Aki Tsuki, Nguyễn Việt Lâm,

Lê Thị Thục Hiền, Nguyễn Trúc Giang, Học 24h, @tth_new, @Akai Haruma

Help me! Cần gấp

thanks!

a.

$x^2-11=0$

$\Leftrightarrow x^2=11$

$\Leftrightarrow x=\pm \sqrt{11}$

b. $x^2-12x+52=0$

$\Leftrightarrow (x^2-12x+36)+16=0$

$\Leftrightarrow (x-6)^2=-16< 0$ (vô lý)

Vậy pt vô nghiệm.

c.

$x^2-3x-28=0$

$\Leftrightarrow x^2+4x-7x-28=0$

$\Leftrightarrow x(x+4)-7(x+4)=0$

$\Leftrightarrow (x+4)(x-7)=0$

$\Leftrightarrow x+4=0$ hoặc $x-7=0$

$\Leftrightarrow x=-4$ hoặc $x=7$

d.

$x^2-11x+38=0$

$\Leftrightarrow (x^2-11x+5,5^2)+7,75=0$

$\Leftrightarrow (x-5,5)^2=-7,75< 0$ (vô lý)

Vậy pt vô nghiệm

e.

$6x^2+71x+175=0$

$\Leftrightarrow 6x^2+21x+50x+175=0$

$\Leftrightarrow 3x(2x+7)+25(2x+7)=0$

$\Leftrightarrow (3x+25)(2x+7)=0$

$\Leftrightarrow 3x+25=0$ hoặc $2x+7=0$

$\Leftrightarrow x=-\frac{25}{3}$ hoặc $x=-\frac{7}{2}$

f.

$x^2-(\sqrt{2}+\sqrt{8})x+4=0$

$\Leftrightarrow x^2-\sqrt{2}x-2\sqrt{2}x+4=0$

$\Leftrightarrow x(x-\sqrt{2})-2\sqrt{2}(x-\sqrt{2})=0$

$\Leftrightarrow (x-\sqrt{2})(x-2\sqrt{2})=0$

$\Leftrightarrow x-\sqrt{2}=0$ hoặc $x-2\sqrt{2}=0$

$\Leftrightarrow x=\sqrt{2}$ hoặc $x=2\sqrt{2}$

g.

$(1+\sqrt{3})x^2-(2\sqrt{3}+1)x+\sqrt{3}=0$

$\Leftrightarrow (1+\sqrt{3})x^2-(1+\sqrt{3})x-(\sqrt{3}x-\sqrt{3})=0$

$\Leftrightarrow (1+\sqrt{3})x(x-1)-\sqrt{3}(x-1)=0$

$\Leftrightarrow (x-1)[(1+\sqrt{3})x-\sqrt{3}]=0$

$\Leftrightarrow x-1=0$ hoặc $(1+\sqrt{3})x-\sqrt{3}=0$

$\Leftrightarrow x=1$ hoặc $x=\frac{3-\sqrt{3}}{2}$

Ta có

\(x=\frac{\sqrt{4+2\sqrt{3}}-\sqrt{3}}{\left(\sqrt{5}+2\right)\sqrt[3]{17\sqrt{5}-38}-2}\)

\(=\frac{\sqrt{3+2\sqrt{3}+1}-\sqrt{3}}{\left(\sqrt{5}+2\right)\sqrt[3]{5\sqrt{5}-3.5.2+3.4.\sqrt{5}-8}-2}\)

\(=\frac{\sqrt{3}+1-\sqrt{3}}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)-2}=\frac{1}{5-4-2}=-1\)

Thế vào ta được

\(P=\left(x^2+x+1\right)^{2013}+\left(x^2+x-1\right)^{2013}\)

\(=\left(1-1+1\right)^{2013}+\left(1-1-1\right)^{2013}=1-1=0\)

a) ĐKXĐ: \(x\ge0\)

Ta có: \(3\sqrt{18x}-5\sqrt{8x}+4\sqrt{50x}=38\)

\(\Leftrightarrow9\sqrt{2x}-10\sqrt{2x}+20\sqrt{2x}=38\)

\(\Leftrightarrow19\sqrt{2x}=38\)

\(\Leftrightarrow\sqrt{2x}=2\)

\(\Leftrightarrow2x=4\)

hay x=2(thỏa ĐK)

b) ĐKXĐ: \(x\ge0\)

Ta có: \(3\sqrt{12x}-2\sqrt{27x}+4\sqrt{3x}=8\)

\(\Leftrightarrow6\sqrt{3x}-6\sqrt{3x}+4\sqrt{3x}=8\)

\(\Leftrightarrow\sqrt{3x}=2\)

\(\Leftrightarrow3x=4\)

hay \(x=\dfrac{4}{3}\)

c) ĐKXĐ: \(x\ge5\)

Ta có: \(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9x-45}=4\)

\(\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\)

\(\Leftrightarrow2\sqrt{x-5}=4\)

\(\Leftrightarrow\sqrt{x-5}=2\)

\(\Leftrightarrow x-5=4\)

hay x=9

a)

\(3.3\sqrt{2x}-5.2\sqrt{2x}+4.5.\sqrt{2x}=38\\ \Leftrightarrow19\sqrt{2x}=38\\ \Leftrightarrow\sqrt{2x}=2\\ \Leftrightarrow x=2\)

b)

\(3.2.\sqrt{3x}-2.3.\sqrt{3x}+4.\sqrt{3x}=8\\ \Leftrightarrow4\sqrt{3x}=8\\ \Leftrightarrow\sqrt{3x}=2\\\Leftrightarrow x=\dfrac{2^2}{3}=\dfrac{4}{3} \)

c)

\(\sqrt{4\left(x-5\right)}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9\left(x-5\right)}=4\\ \Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\\ \Leftrightarrow2\sqrt{x-5}=4\\ \Leftrightarrow x-5=4\\ \Leftrightarrow x=9\)

Lời giải:

a) ĐK: $x\geq \frac{1}{2}$

PT $\Rightarrow 2x-1=(\sqrt{2}-1)^2=3-2\sqrt{2}$

$\Leftrightarrow 2x=4-2\sqrt{2}$

$\Leftrightarrow x=2-\sqrt{2}$ (thỏa mãn)

Vậy.........

b) ĐK: $x\geq \frac{-11}{3}$

PT $\Rightarrow 3x+11=(3+\sqrt{2})^2=11+6\sqrt{2}$

$\Leftrightarrow x=2\sqrt{2}$ (thỏa mãn)

Vậy.........

c)

ĐK: $x\geq -5$

Ta thấy: $\sqrt{x+5}\geq 0$ với mọi $x\geq -5$, mà $\sqrt{3}-2< 0$ nên PT vô nghiệm.

d)

ĐK: $x\geq -38$

PT $\Rightarrow x+38=(3+\sqrt{5})^2=14+6\sqrt{5}$

$\Leftrightarrow x=6\sqrt{5}-24$ (thỏa mãn)

Vậy........

a) \(\sqrt{7-x}+\sqrt{x-5}=x^2-12x+38\)

ĐKXĐ : \(5\le x\le7\)

Bình phương vế trái ta được:

\(VT^2=7-x+x-5+2\sqrt{\left(7-x\right)\left(x-5\right)}\)

       \(=2+2\sqrt{-x^2+12x-35}\)

       \(=2+2\sqrt{1-\left(x^2-12x+36\right)}\)

       \(=2+2\sqrt{1-\left(x-6\right)^2}\le2+2.1=4\)

 => \(VT\le2\) \(\left(VT\ge0\right)\)  (1)

\(VP=x^2-12x+38=\left(x^2-12x+36\right)+2=\left(x-6\right)^2+2\ge2\)  (2)

Từ (1) và (2) suy ra VT=VP=2

=> x=6 (thỏa mãn ĐKXĐ)

Vậy ... 

b)\(\sqrt{x-1}+\sqrt{x+3}+2\sqrt{x^2+2x-3}=4-2x\)

ĐKXĐ : \(x\ge1\)

Với ĐKXĐ ta luôn có: \(VT=\sqrt{x-1}+\sqrt{x+3}+2\sqrt{\left(x-1\right)\left(x+3\right)}\ge\sqrt{4}=2\) (1)

\(VP=4-2x=2\left(2-x\right)\le2\) (2)

Từ (1) và (2) suy ra VT = VP = 2

=> x=1 ( Thỏa mãn ĐKXĐ )

Vậy ...

Câu b) mình làm thấy sai sai ấy. Bạn nào biết vào giải giúp với :) cảm ơn :)