Giúp e câu 1,2 ạ cảm ơn nhiều
AG
Những câu hỏi liên quan
Giúp e câu 1,2 và 4 vs ạ, e cảm ơn
\(\lim\dfrac{\left(3n^2+1\right)\left(1-4n\right)}{n^3-2n+5}=\lim\dfrac{\left(3+\dfrac{1}{n^2}\right)\left(\dfrac{1}{n}-4\right)}{1-\dfrac{2}{n^2}+\dfrac{5}{n^3}}=\dfrac{3.\left(-4\right)}{1}=-12\)
\(\lim\dfrac{\sqrt[]{4n^2-1}+\sqrt[]{n^2-5}}{n+\sqrt[3]{n^3-2n^2}}=\lim\dfrac{\sqrt[]{4-\dfrac{1}{n^2}}+\sqrt[]{1-\dfrac{5}{n^2}}}{1+\sqrt[3]{1-\dfrac{2}{n}}}=\dfrac{\sqrt[]{4}+\sqrt[]{1}}{1+\sqrt[3]{1}}=\dfrac{5}{2}\)
\(\lim\dfrac{\left(3-n\right)^7\left(2+n\right)^3}{\left(n^2+1\right)\left(n^8+3\right)}=\lim\dfrac{\left(\dfrac{3}{n}-1\right)^7\left(\dfrac{2}{n}+1\right)^3}{\left(1+\dfrac{1}{n^2}\right)\left(1+\dfrac{3}{n^8}\right)}=\dfrac{\left(-1\right)^7.1^3}{1.1}=-1\)
Đúng 0
Bình luận (0)
Giúp e câu này với ạ e cảm ơn nhiều
Mn giúp e làm câu 1,3,4 với ạ. E Cảm ơn mn nhiều ạ

dạ câu 18 den 30 e giải không dc ạ giúp e với, e cảm ơn nhiều ạ

Giúp e 2 câu a b với ạ e đang cần rất gấp e cảm ơn mọi người nhiều ạ!
a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)
Đúng 2
Bình luận (0)
Mọi người giúp e câu này với ạ. E cảm ơn moinj người nhiều
Đọc tiếp
Mọi người giúp e câu này với ạ. E cảm ơn moinj người nhiều
Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$
Đúng 1
Bình luận (0)
Giúp 2 câu này đc ko ạ !! e cảm ơn nhiều

Mn giúp e câu 10 với ạ. E cần gấp. Cảm ơn mn rất nhiều
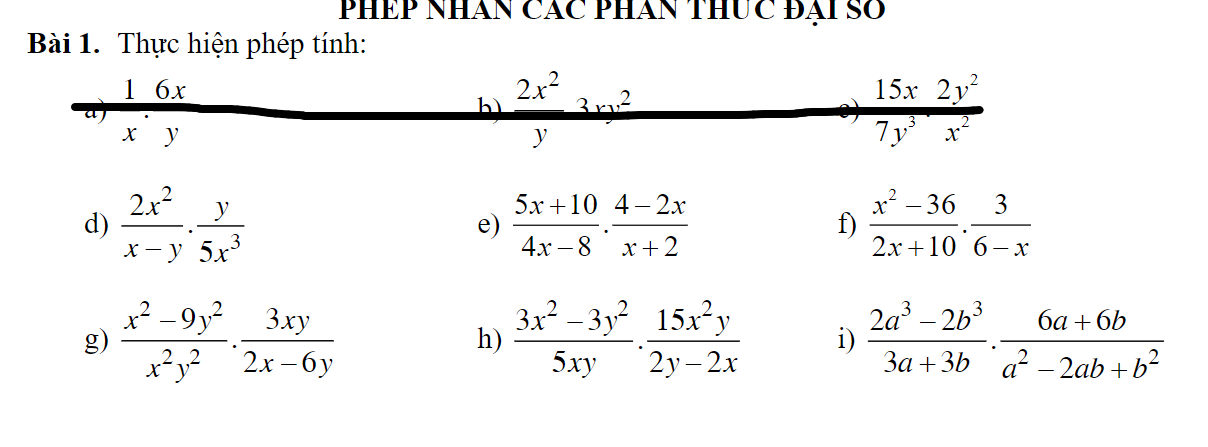
Anh chị giúp e giải câu này với ạ! Em cảm ơn rất nhiều ạ<3
\(d,=\dfrac{3y}{5x\left(x-y\right)}\\ e,=\dfrac{5x\left(x+2\right)\left(2-x\right)}{4\left(x-2\right)\left(x+2\right)}=\dfrac{-5x}{4}\\ f,=\dfrac{3\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)\left(6-x\right)}=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\\ g,=\dfrac{3xy\left(x-3y\right)\left(x+3y\right)}{2x^2y^2\left(x-3y\right)}=\dfrac{3\left(x+3y\right)}{2xy}\\ h,=\dfrac{45x^2y\left(x-y\right)\left(x+y\right)}{10xy\left(y-x\right)}=\dfrac{-9x\left(x+y\right)}{2}\\ i,=\dfrac{12\left(a-b\right)\left(a+b\right)\left(a^2+ab+b^2\right)}{3\left(a+b\right)\left(a-b\right)^2}=\dfrac{4\left(a^2+ab+b^2\right)}{a-b}\)
Đúng 3
Bình luận (0)
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)
Đúng 0
Bình luận (0)



