A = 12 + \(\frac{12}{x-5}\) 

=> Để A có giá trị lớn nhất thì \(\frac{12}{x-5}\)phải có giá trị lớn nhất => x -5 phải có giá trị nhỏ nhất và có cùng dấu với 12(1)

Mà x là số nguyên => x - 5 cũng là 1 số nguyên (2)

Từ (1) và (2) suy ra: (x-5) phải là ước nguyên dương nhỏ nhất của 12 => x - 5 = 1 <=> x = 6

\(B=\frac{37-3x}{10-x}\)

Biến đổi \(B=\frac{37-3x}{10-x}=\frac{3\left(10-x\right)+7}{10-x}=3+\frac{7}{10-x}\)

Xét x > 10 thì B < 0                         (1)

Xét x < 10 thì mẫu 10 - x là số nguyên dương . Phân số B có tử và mẫu đều dương,tử không đổi nên B lớn nhất \(\Leftrightarrow\)mẫu 10 - x nhỏ nhất \(\Leftrightarrow10-x=1\Leftrightarrow x=9\).Khi đó A = 10                (2)

So sánh (1) và (2) , ta thấy GTLN của A là 10 khi và chỉ khi x = 9

b) \(Q=\dfrac{27-2x}{12-x}=\dfrac{2.\left(12-x\right)+3}{12-x}=2+\dfrac{3}{12-x}\)

Để Q đạt max 

thì \(\dfrac{3}{12-x}\) phải max nên 12 - x phải min và 12 - x > 0 

lại có \(x\inℤ\) 

nên 12 - x = 1 

<=> x = 11 

Khi đó Q = 17

Vậy Q_max = 5 khi x = 11 

mik giải theo cái 37-3x/10-x  nha Azure phan bảo linh

cái pải z ko bn

bài toán :

\(\frac{37-3x}{10}-x\)

 Rút gọn biểu thức:

\(\frac{-\left(13x-37\right)}{10}\)

Hoặc là : Phân tích thành nhân tử

\(\frac{18\frac{1}{2}-\frac{13x}{2}}{5}\)\(nha\)

1) \(A=5.\left|x-5\right|-3x+1\)

\(A=\left[{}\begin{matrix}5.\left(x-5\right)-3x+1\left(x-5\ge0\right)\\5.\left(5-x\right)-3x+1\left(x-5< 0\right)\end{matrix}\right.\)

\(A=\left[{}\begin{matrix}5x-25-3x+1\left(x\ge5\right)\\25-5x-3x+1\left(x< 5\right)\end{matrix}\right.\)

\(A=\left[{}\begin{matrix}2x-24\left(x\ge5\right)\\26-8x\left(x< 5\right)\end{matrix}\right.\)

3:

\(Q=\dfrac{27-2x}{12-x}=\dfrac{2x-27}{x-12}\)

\(\Leftrightarrow Q=\dfrac{2x-24-3}{x-12}=2-\dfrac{3}{x-12}\)

Để Q lớn nhất thì \(2-\dfrac{3}{x-12}\) lớn nhất

=>\(\dfrac{3}{x-12}\) nhỏ nhất

=>x-12 là số nguyên âm lớn nhất

=>x-12=-1

=>x=11

Vậy: \(Q_{min}=2-\dfrac{3}{11-12}=2+3=5\) khi x=11

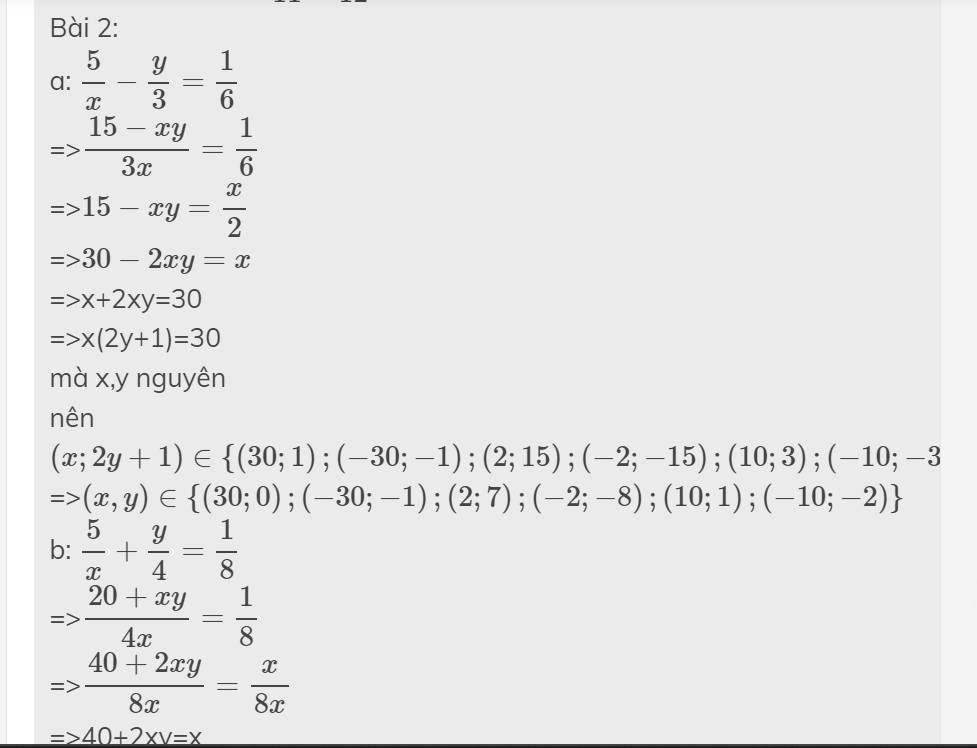
Bài 2:

a: \(\dfrac{5}{x}-\dfrac{y}{3}=\dfrac{1}{6}\)

=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)

=>\(15-xy=\dfrac{x}{2}\)

=>\(30-2xy=x\)

=>x+2xy=30

=>x(2y+1)=30

mà x,y nguyên

nên \(\left(x;2y+1\right)\in\left\{\left(30;1\right);\left(-30;-1\right);\left(2;15\right);\left(-2;-15\right);\left(10;3\right);\left(-10;-3\right)\right\}\)

=>\(\left(x,y\right)\in\left\{\left(30;0\right);\left(-30;-1\right);\left(2;7\right);\left(-2;-8\right);\left(10;1\right);\left(-10;-2\right)\right\}\)

b: \(\dfrac{5}{x}+\dfrac{y}{4}=\dfrac{1}{8}\)

=>\(\dfrac{20+xy}{4x}=\dfrac{1}{8}\)

=>\(\dfrac{40+2xy}{8x}=\dfrac{x}{8x}\)

=>40+2xy=x

=>x-2xy=40

=>x(1-2y)=40

mà x,y nguyên

nên \(\left(x;1-2y\right)\in\left\{\left(40;1\right);\left(-40;-1\right);\left(8;5\right);\left(-8;-5\right)\right\}\)

=>\(\left(x,y\right)\in\left\{\left(40;0\right);\left(-40;1\right);\left(8;-2\right);\left(-8;3\right)\right\}\)

Giup mình với ah.

1- Tính :

A= 5. | x- 5 | - 3x + 1

2 - Tìm các số nguyên x,y ; sao cho :

a) 5/x - y/3 = 1/6                        b) 5/x + y/4 = 1/8

3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)

---------------------------------------------------------------------------------------------

\(P=\dfrac{2x-3}{x-2}=\dfrac{2x-4+1}{x-2}=2+\dfrac{1}{x-2}\)

P max khi x-2=1

=>x=3

A = \(\dfrac{22-3x}{4-x}\)

A = \(\dfrac{3.\left(4-x\right)+10}{4-x}\)

A = 3 + \(\dfrac{10}{4-x}\)

A lớn nhất khi \(\dfrac{10}{4-x}\) lớn nhất. Vì 10 > 0; \(x\) \(\in\) Z nên \(\dfrac{10}{4-x}\) lớn nhất khi

 4 - \(x\) = 1 ⇒ \(x\) = 4 - 1 ⇒   \(x\) = 3

Vậy A_min  = 3 + \(\dfrac{10}{1}\) = 13 khi \(x\) =3

Kết luận giái trị lớn nhất của biểu thức là 13 xảy ra khi \(x\) = 3 

Biểu thức không có max. Bạn coi lại đề.

À ha sorry bạn. Mình quên mất điều kiện $x$ nguyên.

Xét 2 TH sau:

TH1: $x>2$:

$B=\frac{x-1}{x-2}=1+\frac{1}{x-2}$

Để $B$ max thì $\frac{1}{x-2}$ max $\Leftrightarrow x-2$ min 

Vậy $x-2$ phải là số nguyên dương bé nhất, tức là $x-2=1$

$\Leftrightarrow x=3$

Khi đó: \(B_{\max}=\frac{3-1}{|3-2|}=2(*)\)

TH2: $x< 2$

$B=\frac{x-1}{2-x}=-(1+\frac{1}{x-2})$
Để B max thì $1+\frac{1}{x-2}$ min 

$\Leftrightarrow x-2$ max. Mà $x<2$ nên $x-2$ phải là số nguyên âm lớn nhất 

$\Leftrightarrow x-2=-1$

$\Leftrightarrow x=1$

Khi đó: $B=0(**)$

Từ $(*); (**)\Rightarrow B_{\max}=2$ khi $x=3$

\(A=2\left(x^2-4x+4\right)-7=2\left(x-2\right)^2-7\ge-7\)

Dấu \("="\Leftrightarrow x=2\)

\(B=\left(x^2+3x+\dfrac{9}{4}\right)-\dfrac{1}{4}=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

Dấu \("="\Leftrightarrow x=-\dfrac{3}{2}\)

\(C=4\left(x^2-2x+1\right)-4=4\left(x-1\right)^2-4\ge-4\)

Dấu \("="\Leftrightarrow x=1\)

\(D=\dfrac{1}{-\left(x^2+2x+1\right)+6}=\dfrac{1}{-\left(x+1\right)^2+6}\ge\dfrac{1}{6}\)

Dấu \("="\Leftrightarrow x=-1\)

\(A=2\left(x^2-4x+4\right)-7=2\left(x-2\right)^2-7\ge-7\)

\(A_{min}=-7\) khi \(x=2\)

\(B=\left(x^2+3x+\dfrac{9}{4}\right)-\dfrac{1}{4}=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

\(B_{min}=-\dfrac{1}{4}\) khi \(x=-\dfrac{3}{2}\)

\(C=4\left(x^2-2x+1\right)-4=4\left(x-1\right)^2-4\ge-4\)

\(C_{min}=-4\) khi \(x=1\)

Biểu thức D không tồn tại cả max lẫn min

1.

$A=2x^2-8x+1=2(x^2-4x+4)-7=2(x-2)^2-7$

Vì $(x-2)^2\geq 0$ với mọi $x\in\mathbb{R}$

$\Rightarrow A\geq 2.0-7=-7$

Vậy $A_{\min}=-7$ khi $x-2=0\Leftrightarrow x=2$

2.

$B=x^2+3x+2=(x^2+3x+1,5^2)-0,25=(x+1,5)^2-0,25\geq 0-0,25=-0,25$

Vậy $B_{\min}=-0,25$ khi $x=-1,5$

3.

$C=4x^2-8x=(4x^2-8x+4)-4=(2x-2)^2-4\geq 0-4=-4$

Vậy $C_{\min}=-4$ khi $2x-2=0\Leftrightarrow x=1$

4. Để $D_{\min}$ thì $5-x^2-2x$ là số thực âm lớn nhất

Mà không tồn tại số thực âm lớn nhất nên không tồn tại $x$ để $D_{\min}$