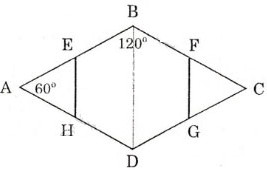
Cho hình thoi ABCD có \(\widehat{A}=60°\). Gọi E; F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. C/m: 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn.
TL
Những câu hỏi liên quan
Cho hình thoi ABCD có \(\widehat{A}=60^0\). Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều ?
ABCD là hình thoi,  =
=  nên
nên 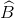 =
=  ,
,  =
=  .
.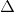 EAH là tam giác đều (vì tam giác cân có một góc
EAH là tam giác đều (vì tam giác cân có một góc  ) nên
) nên 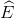 =
=  ,
,  =
=  . Cũng thế
. Cũng thế  =
=  ,
,  =
=  .
.
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
Đúng 0
Bình luận (0)

ABCD là hình thoi,  =
=  nên
nên 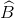 =
=  ,
,  =
=  .
.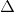 EAH là tam giác đều (vì tam giác cân có một góc
EAH là tam giác đều (vì tam giác cân có một góc  ) nên
) nên 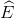 =
=  ,
,  =
=  . Cũng thế
. Cũng thế  =
=  ,
,  =
=  .
.
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thoi ABCD có \(\widehat{A}=60^0\). Gọi O là giao điểm của hai đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA.
Chứng minh rằng 6 điểm E, B, F, G, D, H thuộc cùng một đường tròn ?
Cho hình thoi ABCD có \(\widehat{A}=60^o,AC=a\sqrt{3}.\)Tính theo a độ dài cạnh hình thoi
Cho \(SA\perp\left(ABCD\right)\) ,\(ABCD\) là hình thoi cạnh \(a\),\(SA=a\sqrt[]{2}\) ,\(\widehat{BAD}=60^o\) . Tính \(\widehat{(SAD),(SCD)}\).
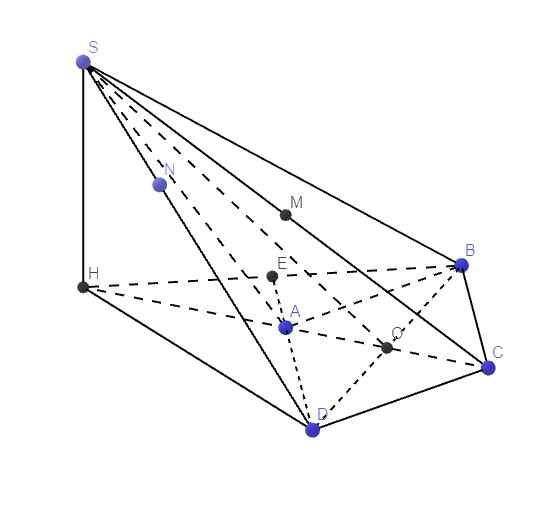
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, widehat{BAD}120^o. Biết SAperp BD,SBperp AD và (SBD) tạo với mặt phẳng (ABCD) góc 60^o. Lấy H đối xứng với C qua A.a) Tính V_{S.ABCD}b) Gọi các điểm M, N lần lượt thuộc các cạnh SC, SD sao cho SMdfrac{asqrt{43}}{4};SNdfrac{asqrt{39}}{6}. Tính V_{AMND}.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, \(\widehat{BAD}=120^o\). Biết \(SA\perp BD,SB\perp AD\) và (SBD) tạo với mặt phẳng (ABCD) góc \(60^o\). Lấy H đối xứng với C qua A.
a) Tính \(V_{S.ABCD}\)
b) Gọi các điểm M, N lần lượt thuộc các cạnh SC, SD sao cho \(SM=\dfrac{a\sqrt{43}}{4};SN=\dfrac{a\sqrt{39}}{6}\). Tính \(V_{AMND}\).
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}=60^0\Rightarrow\) các tam giác ABC và ACD là các tam giác đều
\(AH=AC\Rightarrow AH=AC=AB\Rightarrow\Delta HBC\) vuông tại B
\(\Rightarrow HB\perp BC\Rightarrow HB\perp AD\)
Qua H kẻ đường thẳng \(d\perp\left(ABCD\right)\Rightarrow S\in d\)
Gọi O là giao điểm AC và BD, do góc giữa (SBD) và đáy bằng 60 độ
\(\Rightarrow\widehat{SOH}=60^0\)
\(\Rightarrow SH=OH.tan60^0=\left(AH+AO\right).tan60=\left(a+\dfrac{a}{2}\right).tan60^0=\dfrac{3a\sqrt{3}}{2}\)
\(V_{S.ABCD}=\dfrac{1}{3}SH.S_{ABCD}=\dfrac{1}{3}.\dfrac{3a\sqrt{3}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3}{4}\)
Đúng 3
Bình luận (0)
b.
\(SC=\sqrt{SH^2+HC^2}=\sqrt{SH^2+\left(2AC\right)^2}=\dfrac{a\sqrt{43}}{2}\)
\(\Rightarrow M\) là trung điểm SC \(\Rightarrow AM\) là đường trung bình tam giác SHC
\(\Rightarrow\left\{{}\begin{matrix}AM||SH\Rightarrow AM\perp\left(ABCD\right)\\AM=\dfrac{1}{2}SH=\dfrac{3a\sqrt{3}}{4}\end{matrix}\right.\)
\(HD=\sqrt{OD^2+OD^2}=\sqrt{\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2}=a\sqrt{3}\)
\(\Rightarrow SD=\sqrt{SH^2+HD^2}=\dfrac{a\sqrt{39}}{2}\Rightarrow SN=\dfrac{1}{3}SD\Rightarrow ND=\dfrac{2}{3}SD\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}d\left(S;\left(MAD\right)\right)\)
Mà \(SH||\left(MAD\right)\Rightarrow d\left(S;\left(MAD\right)\right)=d\left(H;\left(MAD\right)\right)\)
Gọi E là giao điểm BH và AD, ta có:
\(\left\{{}\begin{matrix}HB\perp AD\left(cmt\right)\\AM\perp\left(ABCD\right)\Rightarrow AM\perp HB\end{matrix}\right.\) \(\Rightarrow HB\perp\left(MAD\right)\)
\(\Rightarrow HE=d\left(H;\left(MAD\right)\right)\)
\(HE=\dfrac{1}{2}HB=\dfrac{1}{2}HD=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}HE=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{AMND}=\dfrac{1}{3}.d\left(N;\left(MAD\right)\right).\dfrac{1}{2}AM.AD=\dfrac{a^3}{8}\)
Đúng 2
Bình luận (0)
Cho hình thoi ABCD có góc A = 60 độ
a) Tính các góc của hình thoi
b) Gọi E là giao điểm CD. Trên tia đối của tia EB lấy F sao cho EF = EB. Tứ giác BCFD là hình gì?
| Nguyễn Văn Khởi |
| Thứ 7, ngày 25/11/2017lúc 9:30:03 |

Đúng 0
Bình luận (0)
a) \(\widehat{C1}=\widehat{A}=60\)độ
\(\widehat{ABC}=\widehat{ADC}=180-\widehat{A}=180-60=120\)độ ( ABCD - hình thoi )
b) Tứ giác BCFD có
BE = EF ( gt )
CE = ED ( gt )
\(\Rightarrow\)BCFD - hbh ( 1 )
\(\Delta BCD\)có : CB=CD ( ABCD - hình thoi )
Và \(\widehat{C1}=60\)độ ( cmt )
\(\Rightarrow\)\(\Delta BCD\)đều
\(\Rightarrow\)BC = BD ( 2 )
Từ ( 1 ) , ( 2 ) suy ra BCFD - hình thoi
hình vẽ minh họa nên hơi xấu
Đúng 0
Bình luận (0)
| Thứ 3, ngày 29/11/2016 11:18:29 |

làm đúng bn nhỉ mk vừa chụp xong ko chép mạng đâu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có \(\widehat{ABC}\)=60°. Kẻ tia Ax song song với BC. Trên tia Ax lấy điểm D sao cho AD=DC
a) Chứng minh tứ giác ABCD là hình thang cân
b) Gọi E là trung điểm của BC. Chứng minh tứ giác ADEB là hình thoi
c) Cho AC=8cm, AB=5cm. Tính diện tích hình thoi ABED
Cho hình thoi ABCD có góc A = 60 độ. Gọi E là điểm đối xứng của B qua AD. Nối AE, ED. CM rằng:
a) ABDE là hình thoi.
b) Ba điểm E, D, C thẳng hàng.
c) EB = AC
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
⏜
60
°
,
S
A
⊥
A
B
C
D
,
S
A
3
a
2
. Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) ...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A B C ⏜ = 60 ° , S A ⊥ A B C D , S A = 3 a 2 . Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
A. 3 a 4
B. 3 a 8 .
C. 5 a 8
D. 5 a 4 .
Cho hình thoi ABCD có \(\widehat{B}=60\). Một đường thẳng d đi qua D không cắt các cạnh hình thoi và cắt các đường thẳng BA, BC lần lượt tại điểm E và F. Gọi M là giao điểm của 2 đường thẳng AF và CE. Chứng minh rằng:
a/ Tam giác AEC đồng dạng với tam giác CAF.
b/ \(AD^2=AM.AF\)