Cho tứ giác lồi ABCD ( không phải là hình bình hành) ngoại tiếp (O;R). Gọi I là trung điểm của AC; J là trung điểm của BD. Chứng minh I,O,J thẳng hàng
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
HB
Những câu hỏi liên quan
Cho tứ giác ABCD là hình bình hành và B A D ⏜ = 90 0 . Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
A. Trung điểm AC
B. Điểm A
C. Điểm B
D. Điểm D
Đáp án A
Vì tứ giác ABCD là hình bình hành và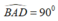 
nên ABCD là hình chữ nhật.
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
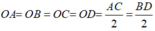
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Đúng 0
Bình luận (0)
Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC. ABCFE có phải là đa giác lồi không? Vì sao?
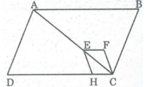
Hình ABCFE không phải là tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.
Đúng 0
Bình luận (0)
Cho tứ giác lồi ABCD. GIẢ SỬ E LÀ ĐIỂM ĐỂ TỨ GIÁC ABDE LÀ HÌNH BÌNH HÀNH. CHỨNG MINH TỨ GIÁC ABCD VÀ TAM GIÁC ACE CÓ DIÊN TÍCH BẰNG NHAU
Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E, F. Các hình đó có phải là đa giác lồi không? Vì sao?
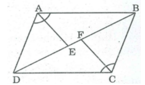
Hình ABCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Hình ADCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Đúng 0
Bình luận (0)
Cho tứ giác lồi ABCD có M, N là trung điểm AB, CD; I, K là trung điểm đường chéo AC, BD. Chứng minh rằng tứ giác MINK là hình bình hành.
Xét ΔABC có
M là trung điểm của AB
I là trung điểm của AC
Do đó: MI là đường trung bình của ΔBAC
Suy ra: MI//BC và \(MI=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
K là trung điểm của BD
N là trung điểm của CD
Do đó: KN là đường trung bình của ΔBDC
Suy ra: KN//BC và \(KN=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra MI=KN và MI//KN
Xét tứ giác MINK có
MI//KN
MI=KN
Do đó: MINK là hình bình hành
Đúng 0
Bình luận (0)
CHO TỨ GIÁC LỒI ABCD
A) CM NẾU MỖI ĐƯỜNG CHÉO PHÂN TỨ GIÁC THÀNH 2 TAM GIÁC CÓ DIỆN TÍCH BẰNG NHAU THÌ ABCD LÀ HÌNH BÌNH HÀNH
B) CM NẾU O LÀ 1 ĐIỂM TRONG TỨ GIÁC SAO CHO SABO=SBCO=SCDO=SDAO THÌ O THUỘC AC HAY O THUỘC BD
Cho hình thang ABCD đáy lớn AD đáy nhỏ BC nội tiếp đường tròn tâm O. AB và CD kéo dài cắt nhau tại I. Các tiếp tuyến của đường tròn (O) tại B và D cắt nhau tại K.a C/m tứ giác BIKD nội tiếpb C/m IK//BCc Hình thang ABCD cần thêm điều kiện gì để tứ giác AIKD là hình bình hành. Khi đó c/m hệ thức: IC.IEID.CE( với E là giao điểm của BK và ID)d Vẽ hình bình hành BDKM, đường tròn ngoại tiếp tam giác BKM cắt đường tròn (O) tại điểm thứ 2N.C/m 3 điểm D,M,N thẳng hàng.
Đọc tiếp
Cho hình thang ABCD đáy lớn AD đáy nhỏ BC nội tiếp đường tròn tâm O. AB và CD kéo dài cắt nhau tại I. Các tiếp tuyến của đường tròn (O) tại B và D cắt nhau tại K.
a> C/m tứ giác BIKD nội tiếp
b> C/m IK//BC
c> Hình thang ABCD cần thêm điều kiện gì để tứ giác AIKD là hình bình hành. Khi đó c/m hệ thức: IC.IE=ID.CE( với E là giao điểm của BK và ID)
d> Vẽ hình bình hành BDKM, đường tròn ngoại tiếp tam giác BKM cắt đường tròn (O) tại điểm thứ 2N.C/m 3 điểm D,M,N thẳng hàng.
Cho em xin đáp án câu c bài này ah
Đúng 0
Bình luận (0)
Cho tứ giác lồi ABCD. GỌI M là một điểm nằm bên trong tứ giác và N là một điểm nằm bên ngoài tứ giác. biết các tứ giác ABMD, BMCN LÀ hình bình hành,. CHỨNG MINH GÓC NAB bằng góc MDC
Cho tứ giác lồi ABCD
a/ C/m nếu mỗi đường chéo phân tứ giác thành 2 tam giác có diện tích bằng nhau thì ABCD là hình bình hành .
b/ C/m nếu O là 1 điểm trong tứ giác sao cho SABO=SBCO=SCDO=SDAO thì O thuộc AC hay O thuộc BD