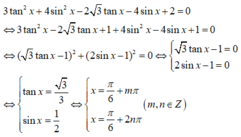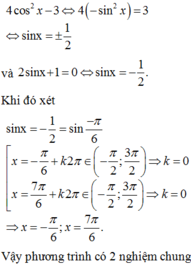4sin2x + 4cos2x - 2√2=0
NH
Những câu hỏi liên quan
Câu 1 : Chứng minh rằng : 3 - 4sin2x = 4cos2x - 1Câu 2 : Chứng minh rằng : cos4x - sin4x = 2cos2x - 1 = 1 - 2sin2xCâu 3 : Chứng minh rằng : sin4x + cos4x = 1 - 2sin2xCos2x
1/ \(3-4\sin^2=4\cos^2x-1\Leftrightarrow4\left(\sin^2x+\cos^2x\right)-4=0\Leftrightarrow4.1-4=0\left(ld\right)\Rightarrow dpcm\)
2/ \(\cos^4x-\sin^4x=\left(\cos^2x+\sin^2x\right)\left(\cos^2x-\sin^2x\right)=\cos^2x-\left(1-\cos^2x\right)=2\cos^2x-1=\left(1-\sin^2x\right)-\sin^2x=1-2\sin^2x\)
3/ \(\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x.\cos^2x=1-2\sin^2x.\cos^2x\)
Đúng 2
Bình luận (0)
Giải phương trình 3tan2x + 4sin2x - 2
3
tanx - 4sinx + 2 0 A. x ±
π
6
+ k2π, k ∈ Z B. x
π
6
+ kπ, k ∈ Z C. x
-
π
4
+ k2π,
-
π
6
+ k2π, k ∈ Z D. Tất cả sai
Đọc tiếp
Giải phương trình 3tan2x + 4sin2x - 2 3 tanx - 4sinx + 2 = 0
A. x = ± π 6 + k2π, k ∈ Z
B. x = π 6 + kπ, k ∈ Z
C. x = - π 4 + k2π, - π 6 + k2π, k ∈ Z
D. Tất cả sai
Số nghiệm chung của hai phương trình
4
cos
2
x
−
3
0
và 2.sin x + 1 0 trên khoảng
−
π
2
;
3
π
2
là...
Đọc tiếp
Số nghiệm chung của hai phương trình 4 cos 2 x − 3 = 0 và 2.sin x + 1 = 0 trên khoảng − π 2 ; 3 π 2 là:
A. 4
B. 1
C. 2
D. 3
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2sinx + l = 0 trên khoảng (-π/2;3π/2) là?
A. 4.
B. 1.
C. 2.
D. 3.
Giải pt ( đưa về pt bậc 2 )
1. tan2x - 5tanx + 6 = 0
2. 3cos22x + 4cos2x + 1 = 0
1.
\(tan^2x-5tanx+6=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=2\\tanx=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arctan\left(2\right)+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)
2.
\(3cos^22x+4cos2x+1=0\)
\(\Rightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=-\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=\pi+k2\pi\\2x=\pm arccos\left(-\dfrac{1}{3}\right)+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{1}{2}arccos\left(-\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải các pt sau:
1) 4sin22x - 5/2sin4x - 6cos22x=0
2) 3sin2x + 4sin2x + (8√3 - 9)cos2x =0
3sin^2x + 4sin2x +(8√3 -9) *cos^2x=0
sin^2 + sin2x - 2cos^2x =1/2
(sinx +1) *( 2cos 2x - 2) =0
giải hộ e bài này vs ạ
a/
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(\Leftrightarrow3tan^2x+8tanx+8\sqrt{3}-9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-\sqrt{3}\\tanx=\frac{3\sqrt{3}-8}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{3}+k\pi\\x=arctan\left(\frac{3\sqrt{3}-8}{3}\right)+k\pi\end{matrix}\right.\)
b/
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^2x\)
\(tan^2x+2tanx-2=\frac{1}{2}\left(1+tan^2x\right)\)
\(\Leftrightarrow tan^2x+4tanx-5=0\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=arctan\left(-5\right)+k\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow\left(sinx+1\right)\left(1-2sin^2x-1\right)=0\)
\(\Leftrightarrow sin^2x\left(sinx+1\right)=0\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
3sin2 + 4sin2x + (8√3 - 9)cos2x = 0 (giải giúp em chi tiết ạ em giải nghiệm ra số rất lẻ )
sinx+ cos+ 1+ sin2x.4cos2x=0
cos4x -4cos2x + cosx -6 = 0
Ta có: \(-1\le cosa\le1\) ; \(\forall a\)
\(\Rightarrow\left\{{}\begin{matrix}cos4x\le1\\-4cos2x\le4\\cosx\le1\end{matrix}\right.\) \(\Rightarrow cos4x-4cos2x+cosx\le6\)
\(\Rightarrow cos4x-4cos2x+cosx-6\le0\)
Dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}cos4x=1\\cos2x=-1\\cosx=1\end{matrix}\right.\)
Phương trình vô nghiệm
Đúng 0
Bình luận (0)