Tìm giá trị lớn nhất và nhỏ nhất của hàm số
y = 3sinx + √3cosx + 2
tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
\(y=\dfrac{sinx+3cosx+1}{sinx-cosx+2}\)
\(ĐK:sinx-cosx\ne-2\)
\(< =>2y-1=sinx\left(1-y\right)+cosx\left(y+3\right)\)
Theo Bunhiacopxki:
\(\left[sinx\left(1-y\right)+cosx\left(y+3\right)\right]^2\)\(\le\left(sin^2x+cos^2x\right)\left[\left(1-y\right)^2+\left(y+3\right)^2\right]\)
\(< =>\left(2y-1\right)^2\le2y^2+4y+10\)
\(< =>2y^2-8y-9\le0\)
=> Bấm máy tìm Max, Min của y
(Sry máy tính của t bị ngáo không bấm ra)
\(\Rightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)
\(\Rightarrow\left(y-1\right)sinx-\left(y+3\right)cosx=1-2y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất
\(\Rightarrow\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2-8y-9\le0\)
\(\Rightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)
\(y_{max}=\dfrac{4+\sqrt{34}}{2}\) ; \(y_{min}=\dfrac{4-\sqrt{34}}{2}\)
\(y=\dfrac{sinx+3cosx+1}{sinx-cosx+2}\)
\(\Leftrightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)
\(\Leftrightarrow\left(y-1\right)sinx-\left(y+3\right).cosx=1-2y\)
Phương trình có nghiệm khi \(\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow y^2-2y+1+y^2+6y+9\ge4y^2-4y+1\)
\(\Leftrightarrow2y^2-8y-9\le0\)
\(\Leftrightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y= 3.(3sinx + 4cosx)2 +4.(3sinx + 4cosx)+ 1
![]()
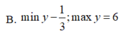
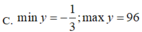
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 sin x + 4 cos x ) 2 + 4 ( 3 sin x + 4 cos x ) + 1
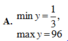
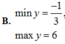
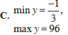
![]()
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3cosx + sinx - 2
![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 sin x + 4 cos x − 1 .
A. max y = 4 , min y = − 6
B. max y = 4 , min y = − 3
C. max y = 2 , min y = − 6
D. max y = 14 , min y = − 6
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sinx+4cosx+1
![]()
![]()

![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=3sinx+4cosx+1
A. max y=4; min y=-4
B. max y=6; min y=-2
C. max y=6; min y=-4
D. max y=6; min y=-1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 sin x + 4 cos x + 1.
A. max y = 4 ; min y = − 4.
B. max y = 6 ; min y = − 2 .
C. max y = 6 ; min y = − 4 .
D. max y = 6 ; min y = − 1 .
Đáp án C
y = 3 sin x + 4 cos x + 1 = 5 sin ( x + α ) + 1 , ( c os α = 3 5 , sin α = 4 5 ) − 1 ≤ sin ( x + α ) ≤ 1 ⇒ − 5 ≤ 5 sin ( x + α ) ≤ 5 ⇒ − 4 ≤ 5 sin ( x + α ) + 1 ≤ 6
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sinx + 4cosx+1
A. max y=4;min y= -4
B. max y=6; min y=-2
C. max y=6; miny =-4
D. max y=6; min y=-1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 s i n x + 4 c o s x ) 2 + 4 3 sin x + 4 cos x + 1
A. min y = 1 3 ; max y = 96
B. min y = - 1 3 ; max y = 6
C. min y = - 1 3 ; max y = 96
D. min y = 2; max y = 6