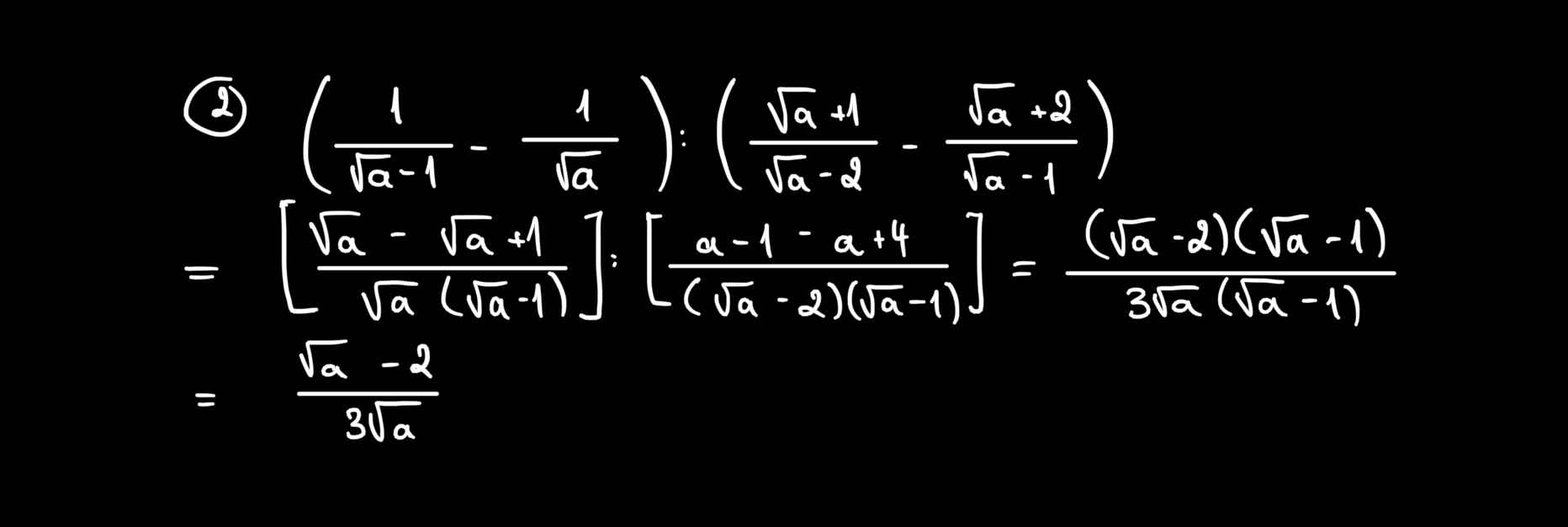\(\sqrt{51-7\sqrt{8}}=\sqrt{7^2-7.2\sqrt{2}+\left(\sqrt{2}\right)^2}=\sqrt{\left(7-\sqrt{2}\right)^2}=7-\sqrt{2}\)

(vì\(7=\sqrt{49}>\sqrt{2}\Rightarrow7-\sqrt{2}>0\))

pt sao có 1 vé vậy bạn

Bạn xem ở đây nhé.

Câu hỏi của Nguyễn Thị Thùy Dung - Toán lớp 9 | Học trực tuyến

1:

ΔABC vuông tại A

=>\(BC^2=AB^2+AC^2\)

=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH\cdot BC=AB\cdot AC\)

=>\(AH\cdot5=3\cdot4=12\)

=>AH=2,4(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)

2:

Chúng ta sẽ gọi AB,AC là hai cạnh góc vuông

AH,AM lần lượt là đường cao và đường trung tuyến kẻ từ A xuống cạnh huyền BC

Theo đề, ta có: AH=4cm và AM=5cm

ΔABC vuông tại A có AM là trung tuyến

nên BC=2*AM

=>BC=10(cm)

Đặt HB=x; HC=y

HB+HC=BC

=>x+y=10(1)

Xét ΔABC vuông tại A có AH là đường cao

nên \(HB\cdot HC=AH^2\)

=>\(x\cdot y=4^2=16\)(2)

Từ (1), (2) suy ra x,y là các nghiệm của phương trình:

\(a^2-10a+16=0\)

=>(a-2)(a-8)=0

=>\(\left[{}\begin{matrix}a=2\\a=8\end{matrix}\right.\)

TH1: \(\left\{{}\begin{matrix}BH=2cm\\CH=8cm\end{matrix}\right.\)

\(AB=\sqrt{BH\cdot BC}=\sqrt{20}=2\sqrt{5}\left(cm\right)\)

\(AC=\sqrt{CH\cdot CB}=\sqrt{8\cdot10}=\sqrt{80}=4\sqrt{5}\left(cm\right)\)

TH2: \(\left\{{}\begin{matrix}BH=8cm\\CH=2cm\end{matrix}\right.\)

\(AB=\sqrt{BH\cdot BC}=4\sqrt{5}\left(cm\right)\)

\(AC=\sqrt{CH\cdot CB}=2\sqrt{5}\left(cm\right)\)

đi cho vui chứ ! mỗi năm được 1 lần mà bạn!!!!

\(\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)

\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\right)\)

\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\left(\dfrac{a-1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{a-4}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\right)\)

\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{3}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)

\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)

Tập xác định của phương trình

Bài toán :

Lời giải: Giải phương trình với tập xác định

Tập xác định của phương trình

Biến đổi vế trái của phương trình

3.              3

Biến đổi vế phải của phương trình

Phương trình thu được sau khi biến đổi

Lời giải thu được

Năm nay mình mới lên lớp 6 thôi, mình chưa học

bài toán nào vậy bạn ?

Được bạn có những bài toán gì ? lớp mấy ? mình chỉ làm được lớp 3 vì mình học lớp 3 

bai toan gi

= 3 nha !

k mik đi

đúng 100% đấy

= 2^10 . ( 13 + 65 ) / 2^8 . 104

= 2^10 . 78 / 2^8 . 104 

= 2 . 2 . 2^8 . 78 / 2^8 . 104

= 2^8 . 312 / 104 

= 3