Tập xác định:y sin√1+x1−xsin1+x1−x là
Đọc tiếp
Tập xác định:
y= là
NN
Những câu hỏi liên quan
Tìm tập xác định D của hàm số
y
1
-
sin
x
1
+
sin
x
Đọc tiếp
Tìm tập xác định D của hàm số y = 1 - sin x 1 + sin x
Tập xác định của hàm số
y
1
+
cos
x
1
-
cos
x
là:
Đọc tiếp
Tập xác định của hàm số y = 1 + cos x 1 - cos x là:
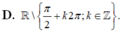
1) Xet x ∈ [\(\dfrac{\Pi}{2}\) ; π ]. Neu x1 < x2 thi Sin x1.......Sin x2
Trên \(\left[\dfrac{\pi}{2};\pi\right]\) hàm \(y=sinx\) nghịch biến nên nếu \(x_1< x_2\Rightarrow sinx_1>sinx_2\)
Đúng 0
Bình luận (0)
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
cho bt: B 12√x−212√x−2- 12√x+212√x+2 +√x1−x√x1−x tìm tập xác định và rút gọn B
Đọc tiếp
cho bt: B= - + tìm tập xác định và rút gọn B
Mình không nhìn thấy đc đề bạn ơi, bạn xem lại đề !!
Đúng 0
Bình luận (3)
1) đa thức f(x)=x^6-x^3+x^2-x+1 có hay ko có nghiệm trên tập hợp số thưc r
2)cho hàm số f(x) xác định với mọi x khác thỏa mãn : f(1)=1 và f(x1 +x2)=f(x1)+f (x2)với mọi x1,x2 jkhacs 0 , x1 + x2 cũng khác 0 và f (1/x)=1/x^2 . f(x) . CMR : f)5/7)=5/7
Cho f(x) xác định với moi x khác 0 thỏa mãn
f(1)=1
f(1/x)=1/x^2
f(x1+x2)=f(x1)+f(x2) với mọi x1,x2 khác 0 vá x1+x2 khác 0
tính f(5/7)
Cho phương trình
cos
x
+
sin
x
1
+
sin
2
x
+
cos
2
x
. Nghiệm của phương trình có dạng
x
1
a
π
+
k
π
.
x
2
±
b
π
+
k
2
π
b
0
Tính tổng a + b A. ...
Đọc tiếp
Cho phương trình cos x + sin x = 1 + sin 2 x + cos 2 x . Nghiệm của phương trình có dạng x 1 = a π + k π . x 2 = ± b π + k 2 π b > 0 Tính tổng a + b
A. 1 12
B. 3
C. 7 π 12
D. π 4
cho hàm số f(x) xác định với mọi x khác 0 thỏa mãn
a) f(1)=1
b)f(1/x)=1/x^2.f(x)
c) f(x1+x2)=f(x1)+f(x2) với mọi x1 , x2 khác 0 , x1+x2 khác 0 . CTR f(5/7)=5/7
Theo c) \(f\left(\frac{5}{7}\right)=f\left(\frac{2}{7}+\frac{3}{7}\right)=f\left(\frac{2}{7}\right)+f\left(\frac{3}{7}\right)\)
\(f\left(\frac{2}{7}\right)=f\left(\frac{1}{7}+\frac{1}{7}\right)=f\left(\frac{1}{7}\right)+f\left(\frac{1}{7}\right)=2.f\left(\frac{1}{7}\right)\)
\(f\left(\frac{3}{7}\right)=f\left(\frac{1}{7}+\frac{2}{7}\right)=f\left(\frac{1}{7}\right)+f\left(\frac{2}{7}\right)=f\left(\frac{1}{7}\right)+2f\left(\frac{1}{7}\right)=3.f\left(\frac{1}{7}\right)\)
\(\implies\)\(f\left(\frac{5}{7}\right)=5.f\left(\frac{1}{7}\right)\) (1)
Theo b) \(f\left(\frac{1}{7}\right)=\frac{1}{7^2}.f\left(7\right)\) (2)
Theo c) \(f\left(7\right)=f\left(3+4\right)=f\left(3\right)+f\left(4\right)\)
\(=2.f\left(3\right)+f\left(1\right)\)
\(=6.f\left(1\right)+f\left(1\right)\)
\(=7.f\left(1\right)\)
Theo a)\(f\left(1\right)=1\)\(\implies\)\(f\left(7\right)=7\) (3)
Từ (1);(2);(3)
\(\implies\) \(f\left(\frac{5}{7}\right)=\frac{5}{7}\)
Xét các khẳng định sau i) Nếu hàm số yf(x) có đạo hàm dương với mọi x thuộc tập số D thì
f
x
1
f
x
2
∀
x
1
,
x
2
∈
D
,
x
1
x
2
ii) Nếu hàm số yf(x) có đạo hàm âm với...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc tập số D thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
ii) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc tập số D thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
iii) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc R thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
iv) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc R thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
Số khẳng định đúng là
A. 1
B. 2
C. 3
D. 4
