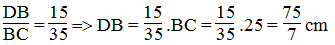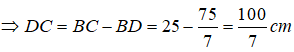Cho tam giác ABC có AB =48cm BC =50cm AC =14cm Gọi CD là phân giác của tam giác ABC tính độ dài CD
H24
Những câu hỏi liên quan
Cho tam giác ABC có BC = 50cm; AC = 14cm; AB = 48cm. Kẻ phân giác CD của góc C, kẻ AH vuông góc với CD tại H. Tính độ dài AD, CD, AH.
Cho tam giác ABC có AB = 48cm, BC = 50cm, AC = 14cm. Tính độ dài phân giác giác góc C
Xét tam giác ABC, ta có
BC2 = 502 = 2500
AB2 + AC2 = 142 + 482 = 2500
=> BC2 = AB2 + AC2
=> Tam giác ABC vuông tại A
Có DA/DB = CA/CB = 14/50 = 7/25 (tính chất tia phân giác)
=> DB = 25/7 DA.
Ta có DA + DB = AB
⇔ DA + 25/7 DA = AB ⇔ DA. 32/7 = 48 ⇔ DA = 10,5cm
Xét tam giác vuông ACD, theo đinh lí Pi-ta-go ta có:
CD2 = AC2 + AD2 = 142 + 10,52 = 306,25 => CD = 17,5cm
Đúng 1
Bình luận (0)
Cho ∆ABC , đường phân giác góc C cắt AB tại D , kẻ AH vuông góc CD . Biết AB = 48cm , BC = 50cm , AC = 14cm . Tính độ dài AD , CD , AH
Cho tam giác ABC có BC15 cm, AC20 cm, AB25 cm.a. Tính độ dài đường cao CH của tam giác ABC.b. Gọi CD là đường phân giác của tam giác ACH. Chứng minh tam giác BCD cân.c. Chứng minh: BC^2+CD^2+BD^23CH^2+2BH^2+DH^2
Đọc tiếp
Cho tam giác \(ABC\) có \(BC=15\) \(cm\), \(AC=20\) \(cm\), \(AB=25\) \(cm\).
\(a\). Tính độ dài đường cao \(CH\) của tam giác \(ABC\).
\(b\). Gọi \(CD\) là đường phân giác của tam giác \(ACH\). Chứng minh tam giác \(BCD\) cân.
\(c\). Chứng minh: \(BC^2+CD^2+BD^2=3CH^2+2BH^2+DH^2\)
a: Xét ΔCAB có CA^2+CB^2=AB^2
nên ΔCAB vuông tại C
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: góc BCD+góc ACD=90 độ
góc BDC+góc HCD=90 độ
mà góc ACD=góc HCD
nên góc BCD=góc BDC
=>ΔBDC cân tại B
c: BC^2+BD^2+CD^2
=BC^2+BC^2+CD^2
=2BC^2+CD^2
=2(BH^2+HC^2)+CH^2+HD^2
=2BH^2+3CH^2+DH^2
Đúng 2
Bình luận (0)
Cho tam giác ABC có BC15 cm, AC20 cm, AB25 cm.
a. Tính độ dài đường cao CH của tam giác ABC.
b. Gọi CD là đường phân giác của tam giác ACH. Chứng minh tam giác BCD cân.
c. Chứng minh: BC^2+CD^2+BD^23CH^2+2BH^2+DH^2
Đọc tiếp
Cho tam giác \(ABC\) có \(BC=15\) \(cm\), \(AC=20\) \(cm\), \(AB=25\) \(cm\).
\(a\). Tính độ dài đường cao \(CH\) của tam giác \(ABC\).
\(b\). Gọi \(CD\) là đường phân giác của tam giác \(ACH\). Chứng minh tam giác \(BCD\) cân.
\(c.\) Chứng minh: \(BC^2+CD^2+BD^2=3CH^2+2BH^2+DH^2\)
Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: (tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:
Đúng 1
Bình luận (0)
Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: (tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:
Đúng 0
Bình luận (0)
Vào trang cá nhân của mik để tham khảo nhé, mik gửi ko có đc
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1.Cho tam giác abc, m là trung điểm của BC, AN là phân giác của góc BAC, BN vuông góc với AN. Biết AB=14cm, AC=19cm. Tính MN
2. Gọi O là giao điểm của 2 đường chéo hình thang cân ABCD (AB//CD, AB>CD). Gọi I, J, K lần lượt là trung điểm của OD, OA, BC. Biết góc AOB=60 độ. Chứng minh tam giác IJK đều.
Cho tam giác abc có BC=15 cm AC=20 cm AB =25 cm. a)Tính độ dài đường cao CH của tam giác ABC b)Gọi CD là phân giác của ACH.Chứng minh tam giác BCD cân c)Chứng minh BC2+CD2+BD2=3.CH2+2.BH2+DH2
Cho tam giác ABC có AB=2cm,AC=3cm,BC=4cm,phân giác AD. Tính độ dài của BD và CD
Ta có: \(BD+CD=BC=4\)
\(\Rightarrow BD=4-CD\)
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}\Rightarrow\dfrac{4-CD}{2}=\dfrac{CD}{3}\)
\(\Rightarrow12-3CD=2CD\)
\(\Rightarrow CD=\dfrac{12}{5}\left(cm\right)\)
\(BD=4-CD=\dfrac{8}{5}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB bằng 4 cm AC bằng 12 cm BC = 6 cm các đường phân giác trong AD be cắt AB tại I
a, Tính BD và CD
b, Gọi AM là đường trung tuyến và G là trọng tâm tam giác ABC . C/m IG//BC và tính độ dài IG
Cho tam giác ABC có BC = 15cm, AC = 20cm, AB = 25cm
a, Tính độ dài đường cao CH của tam giác ABC
b, Gọi CD là đường phân giác của tam giác ACH. CMR: Tam giác BCD cân
c, CMR: BC2 + CD2 + BD2 = 3CH2 + 2BH2 + DH2