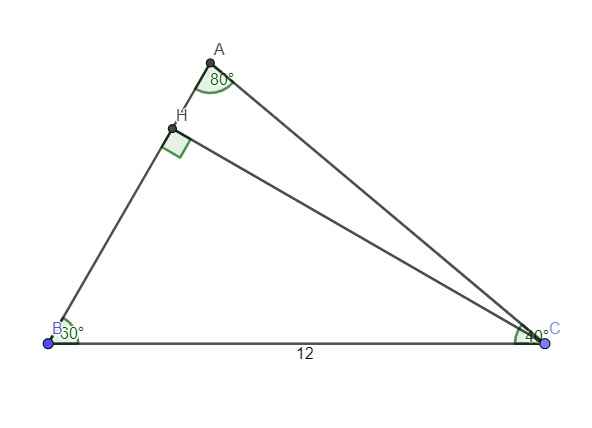
Cho Tam giác ABC có AB=12cm B=60 độ C=40 độ đường cao AH. Tính độ dài AH,AC,BC
MT
Những câu hỏi liên quan
tam giác ABC có B + C = 60 độ , AB = 8cm . Số đo cạnh AC là ??
tam giác ABC có A = 120 ĐỘ ,AB = AC ,BC = 12CM .Độ dài đường cao AH là ???
Cho tam giác ABC có BC=9cm, góc B = 60 độ, góc C=40 độ, đường cao AH. Tính AH, AB, AC
AB = BH . BC = 9.BH
mà BH = \(\dfrac{1}{2}AB\) => AB = 4,5 . AB
=> AB= 4,5
=> BH = 2,25 => HC = 6,75
Tam giác ABH vuông tại H =>AH=\(\dfrac{9\sqrt{3}}{4}\)
Tam giác AHC vuông tại H => AC=\(\dfrac{9\sqrt{3}}{2}\)
Đúng 0
Bình luận (2)
1, cho tam giác ABC có góc A tù, góc C = 30 độ, AB=29 , AC =40. Vẽ đường cao AH. Tính độ dài BH
2, Cho tam giác ABC có AB= 25 , AC = 26. Đường cao AH= 24cm . Tính độ dài BC theo 2 trường hợp
ssssssssssssssssssssssssssssssssssssssssssssssssss
2.cho tam giác ABC có AB= 12cm, góc ABC = 40 độ , góc ACB =30 độ , đường cao AH .Tính AH, AC
Lời giải:
Xét tam giác vuông $ABH$:
$\frac{AH}{AB}=\sin B\Rightarrow AH=AB.\sin B=12.\sin 40^0=12\sin 40^0=7,71$ (cm)
Xét tam giác vuông $AHC$:
$\frac{AH}{AC}=\sin C\Rightarrow AC=\frac{AH}{\sin C}=\frac{7,71}{\sin 30^0}=15,42$ (cm)
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A , có AB=12cm , AC=16cm kẻ đường cao AH (H thuộc BC)
a)chứng minh tam giác HBA đồng dạng tam giác ABC
b)tính độ dài đoạn thẳng BC,AH
đề có vấn đề đấy bạn, ABC cân A thì AB =AC =12 cm chứ sao AC =16cm đc nhỉ
Đúng 0
Bình luận (0)
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
DO đó: ΔHBA∼ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có B=60 độ , C=40 độ ,và BC=12cm. Tính độ dài đường cao CH ,độ dài AC và diện tích tam giác ABC. Mn giúp mình vói nhé và có cả hình
Ta có: \(A=180^0-\left(B+C\right)=80^0\)
Trong tam giác vuông BCH:
\(sinB=\dfrac{CH}{BC}\Rightarrow CH=BC.sinB=12.sin60^0=6\sqrt{3}\left(cm\right)\)
\(cotB=\dfrac{BH}{CH}\Rightarrow BH=CH.cotB\) (1)
Trong tam giác vuông ACH:
\(sinA=\dfrac{CH}{AB}\Rightarrow AB=\dfrac{CH}{sinA}=\dfrac{6\sqrt{3}}{sin80^0}\approx10,6\left(cm\right)\)
\(cotA=\dfrac{AH}{CH}\Rightarrow AH=CH.cotA\) (2)
(1);(2) \(\Rightarrow AH+BH=CH\left(cotA+cotB\right)\)
\(\Rightarrow AB=CH\left(cotA+cotB\right)\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}CH.AB=\dfrac{1}{2}.CH^2\left(cotA+cotB\right)=\dfrac{1}{2}.\left(6\sqrt{3}\right)^2\left(cot80^0+cot60^0\right)\approx40,7\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 5cm, AC = 12cm, BC = 13cm.
a,Chứng minh tam giác ABC⊥ tại A và tính số đo góc B và C
b, Kẻ đường cao AH . Tính độ dài đường cao AH
c.kẻ HE⊥AB tại E ,HF ⊥ AC tại F Chứng minh AE.AB = AF.AC.
cho tam giác vuông tại A,đường cao AH
a,cho biết AB = 3cm,BC = 5cm. Tính độ dài các đoạn thẳng BH,CH,AH và AC
b,cho biết AH = 60cm,CH = 144cm. Tính độ dài các đoạn thẳng AB,AC,BC và BH
c,cho biết AC = 12cm,AH = \(\dfrac{60}{13}cm.\) Tính độ dài các đoạn thẳng AB,BC<BH và CH
a: AC=căn 5^2-3^2=4cm
AH=3*4/5=2,4cm
BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
b: \(BH=\sqrt{60^2:144}=5\left(cm\right)\)
BC=144+5=149cm
\(AB=\sqrt{5\cdot149}=\sqrt{745}\left(cm\right)\)
\(AC=\sqrt{144\cdot149}=12\sqrt{149}\left(cm\right)\)
c: \(HC=\sqrt{AC^2-AH^2}=\dfrac{144}{13}\left(cm\right)\)
\(BH=\dfrac{AH^2}{HC}=\dfrac{25}{13}cm\)
BC=BH+CH=13(cm)
AB=căn 13^2-12^2=5cm
Đúng 0
Bình luận (0)
a
Áo dụng đl pytago vào tam giác ABC vuông tại A:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
\(CH=BC-BH=5-1,8=3,2\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{3.4}{5}=2,4\left(cm\right)\)
b
Áp dụng đl pytago vào tam giác AHC vuông tại H có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{60^2+144^2}=156\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A, đường cao AH có:
\(AC^2=HC.BC\Rightarrow BC=\dfrac{AC^2}{HC}=\dfrac{156^2}{144}=169\left(cm\right)\)
\(BH=BC-HC=169-144=25\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow AB=\sqrt{25.169}=65\left(cm\right)\)
c
Áp dụng đl pytago vào tam giác AHC vuông tại H:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{12^2-\left(\dfrac{60}{13}\right)^2}=\dfrac{144}{13}\approx11,08\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC đường cao AH có:
\(AH^2=HB.HC\Rightarrow HB=\dfrac{AH^2}{HC}=\dfrac{\left(\dfrac{60}{13}\right)^2}{\dfrac{144}{13}}=\dfrac{25}{13}\approx1,92\left(cm\right)\)
\(BC=HB+HC=\dfrac{25}{13}+\dfrac{144}{13}=13\left(cm\right)\)
\(AB^2=HB.BC\Rightarrow AB=\sqrt{HB.HC}=\sqrt{\dfrac{144}{13}.\dfrac{25}{13}}=\dfrac{60}{13}\approx4,62\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có BC = 9cm, góc B= 60 độ, góc C= 40 độ, đường cao AH. Tính AH, AB, AC ( làm tròn đến chữ số thập phân thứ 2)
Giúp với akk mình cần gấp
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, BC = 10cm
a) Tính độ dài AC.
b) Tính diện tích tam giác ABC.
c) Tính độ dài đường cao AH.
a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
Đúng 0
Bình luận (1)