Chú ý : Chứng minh theo trường hợp C.C.C
DN
Những câu hỏi liên quan
Bài 2: Cho tam giác ABC vuông tại A , AB = 8cm, AC = 6cm .
a) Tính BC .
b) Trên cạnh AC lấy điểm E sao cho AE = 2cm; trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ∆BEC = ∆DEC theo trường hợp ( c.c.c ) , ( c.g.c ) , ( g.c.g )
a: BC=căn 8^2+6^2=10cm
b: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
=>ΔCAB=ΔCAD
=>CB=CD và góc ACB=góc ACD
Xét ΔBEC và ΔDEC có
CB=CD
góc BCE=góc DCE
CE chung
=>ΔBEC=ΔDEC(c-g-c)
Xét ΔEDB có
EA vừa là đường cao, vừa là trung tuyến
=>ΔEDB cân tại E
=>ED=EB
Xét ΔCDE và ΔCBE có
CD=CB
DE=BE
CE chung
=>ΔCDE=ΔCBE(c-c-c)
góc CDE+góc EDA=góc CDA
góc CBE+góc EBA=góc CBA
mà góc CDA=góc CBA và góc EDB=góc EBD
nên góc CDE=góc CBE
Xét ΔCEB và ΔCED có
góc CBE=góc CDE
BC=DC
góc BCE=góc DCE
=>ΔCEB=ΔCED
Đúng 0
Bình luận (0)
cho tam giác mnp và tam giác def có mn = de,pm = df. cần thêm điều kiện gì để tam giác mnp và tam giác def bằng nhau theo trường hợp ( c.c.c )
Để hai tam giác trên bằng nhau theo trường hợp c.c.c thì các cặp cạnh tương ứng phải bằng nhau. Vì đã có hai cặp cạnh tương ứng là MN và DE, PM và DF nên cần thêm điều kiện NP = EF để hai tam giác trên bằng nhau theo trường hợp c.c.c
Đúng 0
Bình luận (0)
Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số
f
x
o
+
∆
x
-
f
x
o...
Đọc tiếp
Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số f x o + ∆ x - f ' x o ∆ x khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.
Với Δx > 0 Ta có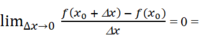 
f'(xo+ ).
Với Δx < 0 Ta có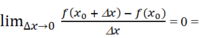 
f'(xo- ).
Vậy f’(xo) = 0.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC. M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC theo 3 cách: c.c.c; c.g.c; g.c.g.
Trong tam giác ABC có:
\(AB=AC\Rightarrow\)Tam giác ABC cân
C1:
Xét 2 tam giác ABM và tam giác ACM có:
AB=AC(gt)
AM(chung)
BM=CM
\(\Rightarrow\)Tam giác ABM=ACM(c.c.c)
\(\Rightarrow\)Góc AMB = góc AMC(tương ứng)
Mà AMB+AMC=180 độ
\(\Rightarrow\)AMB=AMC=90 độ
\(\Leftrightarrow\)AM vuông góc với BC
C2,C3 tương tự
Đúng 0
Bình luận (0)
Cho góc xoy 140,OA vuông góc với Ox,OB vuông góc với Oy,có OC là tia phân giác của góc AOB.Chứng minh tam giác AOC bằng tam giác BOC, theo trường hợp nào dưới đây:
A)C.C.C ;B) C.G.C C) G.C.G D) Cạnh huyền góc vuông
Viết đoạn văn biểu cảm hoặc chứng minh khoảng 10 câu theo lối lập luận diễn dịch (chú ý sử dụng trạng ngữ)
Trường hợp đồng nhất của tam giác (c.c.c)
Cho tam giác ABCD có AB = 8cm; BC = 3cm; CD = 2cm; AD = 6cm và BD = 4cm. Chứng minh:
a)\(\Delta\)ADB\(\sim\)\(\Delta\)BDC;
b)ABCD là hình thang
nêu tính chất các trường hợp bằng nhau của hai tam giác (c.c.c); (c.g.c); (g.c.g)
Chứng minh rằng : T = n2 + 4n + 5 ko chia hết cho 8 . Chú ý n là số lẻ
Chú ý : Các bạn phải làm theo quy trình và giải ra chứ ko đc ghi mỗi đáp án. Và phải giải theo cách của lớp 6
Các bạn làm đúng mình sẽ tick 3 hay 5 tick cho !!!!!!!
Chúc các bạn làm tốt !
Nếu n là số lẻ thì
n2 chia 8 dư 1
4n chia 8 dư 4
5 chia 8 dư 5
=> (1 + 4 + 5) không chia hết cho 8
=>n2 + 4n + 5 không chia hết cho 8 với n là số lẻ
Đúng 0
Bình luận (0)
Cho y ∈ Z, so sánh 100.y với 0
(chú ý: xét mọi trường hợp xảy ra)
Nếu y > 0 thì 100.y > 0
Nếu y = 0 thì 100.y = 0
Nếu y < 0 thì 100.y < 0
Đúng 0
Bình luận (0)