1) Xét ΔABC và ΔABD có
AB chung
AC = AD (gt)
BC = BD (gt)
=> ΔABC = ΔABD (c.c.c)
2) Xét ΔMNA và ΔMNB có
MN chung
MA = MB (gt)
NA = NB (gt)
=> ΔMNA = ΔMNB (c.c.c)
3) Xét ΔDAE và ΔDBE có
DE chung
DA = DB (gt)
EA = EB (gt)
=> ΔDAE = ΔDBE (c.c.c)
Bài 2: Cho tam giác ABC vuông tại A , AB = 8cm, AC = 6cm .
a) Tính BC .
b) Trên cạnh AC lấy điểm E sao cho AE = 2cm; trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ∆BEC = ∆DEC theo trường hợp ( c.c.c ) , ( c.g.c ) , ( g.c.g )
cho tam giác mnp và tam giác def có mn = de,pm = df. cần thêm điều kiện gì để tam giác mnp và tam giác def bằng nhau theo trường hợp ( c.c.c )
Cho tam giác ABC có AB = AC. M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC theo 3 cách: c.c.c; c.g.c; g.c.g.
Cho góc xoy 140,OA vuông góc với Ox,OB vuông góc với Oy,có OC là tia phân giác của góc AOB.Chứng minh tam giác AOC bằng tam giác BOC, theo trường hợp nào dưới đây:
A)C.C.C ;B) C.G.C C) G.C.G D) Cạnh huyền góc vuông
Cho ΔABC có AB = AC, kẻ BD ⊥ AC, CE ⊥ AB D ∈ AC, E ∈ AB. Gọi O là giao điểm của BD và CE. Chứng minh
a) BD = CE (Gợi ý chứng minh ΔBDC ΔCEB theo trường hợp cạnh huyền - góc nhọn).
b) ΔOEB = ΔODC.
c) AO là tia phân giác của ∠BAC.
(Vẽ hình cho mình chép nha!!! Mai mình phải nộp rồi!!! T.T)
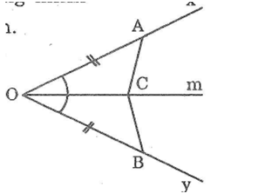
Dựa vào hình dưới, hãy nêu đề toán chứng minh ΔAOC=ΔBOC theo trường hợp cạnh-góc-cạnh.
cho đường thẳng d là đường trung trực AB . M;N thuộc d . chứng minh tam giác AMN = tam giác BMN bằng 3 cách (g.c.g ; c.c.c; c.g.c)
Giúp mk với
Cho tam giác ABC, AM là tia phân giác của góc A, BM =MC. Chứng minh AB = AC, (Lưu ý: Không dùng các trường hợp bằng nhau của tam giá vuông).
Cho tam giác ABC nhọn có AB<AC. Trên cạnh AC lấy E sao cho AB=AE. Gọi H là trung điểm BE.
1) Chứng minh tam giác ABH=AEH (c.c.c)
2) Chứng minh AH vuông góc BE
3) Trên AH lấy điểm F sao AH=HF. Kẻ Ax // BC. Trên Ax lấy I sao AI=BE (I cùng phía với AH). Chứng minh rằng:
a) Chứng minh BF=AE
b) Chứng minh 3 điểm I, B, F thẳng hàng
Cho tam giác ABC nhọn có AB<AC. Trên cạnh AC lấy E sao cho AB=AE. Gọi H là trung điểm BE. 1) Chứng minh tam giác ABH=AEH (c.c.c) 2) Chứng minh AH vuông góc BE 3) Trên AH lấy điểm F sao AH=HF. Kẻ Ax // BC. Trên Ax lấy I sao AI=BE (I cùng phía với AH). Chứng minh rằng: a) Chứng minh BF=AE b) Chứng minh 3 điểm I, B, F thẳng hàng ( kẻ hình nữa nhé )
cảm ơn các bạn nhiều , lm nhanh nhất có thể giúp mik nhé 
