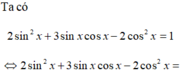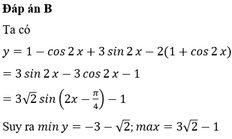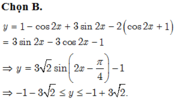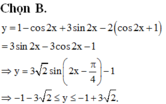4√3sinxcosx + 4cos2x= 2sin2x +5/2
1H
Những câu hỏi liên quan
Phương trình 2 sin 2 x + 3 sin x cos x + cos 2 x = 0 có bao nhiêu nghiệm thuộc (-π/2;π)
A. 0
B. 1
C. 2
D. 4
Hàm số y 2sin2x + 4cos2x + 6sinxcosx tuần hoàn với chu kì: A.
π
2
B. 2π C. π D.
3
π
2
Đọc tiếp
Hàm số y = 2sin2x + 4cos2x + 6sinxcosx tuần hoàn với chu kì:
A. π 2
B. 2π
C. π
D. 3 π 2
Đáp án C
+ y = 2sin2x + 4cos2x + 6sinxcosx = 3sin 2x + cos 2x + 3
+ Hàm số y = 3sin 2x tuần hoàn với chu kì 2π/2 = π.
+ Hàm số y = cos 2x tuần hoàn với chu kì 2π/2 = π.
+ Do đó hàm số y = 2sin2x + 4cos2x + 6sinxcosx là hàm tuần hoàn với chu kì π
Đúng 0
Bình luận (0)
Khi đặt t tan x thì phương trình
2
sin
2
x
+
3
sin
x
cos
x
-
2
cos
2
x
1
trở thành phương trình nào sau đây? A.
2
t
2
-
3
t
-
1
0
B.
3
t...
Đọc tiếp
Khi đặt t = tan x thì phương trình 2 sin 2 x + 3 sin x cos x - 2 cos 2 x = 1 trở thành phương trình nào sau đây?
A. 2 t 2 - 3 t - 1 = 0
B. 3 t 2 - 3 t - 1 = 0
C. 2 t 2 + 3 t - 3 = 0
D. t 2 + 3 t - 3 = 0
CỨU MÌNH VS
a) 3Cos^2x -2Sin2x + Sin^2x =1
b) 4Cos^2x -3SinxCosx +3Sin^2x =1
a/
\(\Leftrightarrow3cos^2x-4sinx.cosx+1-cos^2x=1\)
\(\Leftrightarrow2cos^2x-4sinx.cosx=0\)
\(\Leftrightarrow2cosx\left(cosx-2sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\tanx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=arctan\left(\frac{1}{2}\right)+k\pi\end{matrix}\right.\)
b.
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^2x\)
\(4-3tanx+3tan^2x=1+tan^2x\)
\(\Leftrightarrow2tan^2x-3tanx+3=0\)
Pt vô nghiệm
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
2
s
i
n
2
x
+
3
s
i
n
2
x
-
4
c
o
s
2
x
A. miny -
3
2
-1;maxy
3
2
+1 B. miny -
3
2
-1;maxy ...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 2 s i n 2 x + 3 s i n 2 x - 4 c o s 2 x
A. miny= - 3 2 -1;maxy= 3 2 +1
B. miny= - 3 2 -1;maxy= 3 2 -1
C. miny= - 3 2 ;maxy= 3 2 -1
D. miny= - 3 2 -2;maxy= 3 2 -1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
y
2
sin
2
x
+
3
sin
2
x
-
4
cos
2
x
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y = 2 sin 2 x + 3 sin 2 x - 4 cos 2 x
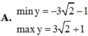
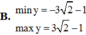
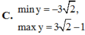
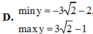
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
y
2
sin
2
x
+
3
sin
2
x
-
4
cos
2
x
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y = 2 sin 2 x + 3 sin 2 x - 4 cos 2 x
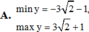
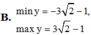
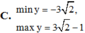
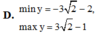
1. sin^8(x) - cos^8(x) - 4sin^6(x) + 6sin^4(x) - 4sin^2(x) = 1
2. sin6x+sin4x+sin2x/1+cos2x+cos4x = 2sin2x
3. 1+sin2x /cosx+sinx - 1-tan^2(x/2)/1+tan^2(x/2) = sinx
4. cos4x + 4cos2x + 3 = 8cos^4(x)
5. 1+cosx+cos2x+cos3x/ 2cos^2(x)+cosx-1 = 2cosx
1. sin^8(x) - cos^8(x) - 4sin^6(x) + 6sin^4(x) - 4sin^2(x) = 1
2. sin6x+sin4x+sin2x/1+cos2x+cos4x = 2sin2x
3. 1+sin2x /cosx+sinx - 1-tan^2(x/2)/1+tan^2(x/2) = sinx
4. cos4x + 4cos2x + 3 = 8cos^4(x)
5. 1+cosx+cos2x+cos3x/ 2cos^2(x)+cosx-1 = 2cosx
\(sin^8x-cos^8x-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-sin^2x\right)^4-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-4sin^2x+6sin^4x-4sin^6x+sin^8x\right)-4sin^6x+6sin^4x-4sin^2x\)\(=-1\) (bạn chép nhầm đề)
b/ \(\frac{sin6x+sin2x+sin4x}{1+cos2x+cos4x}=\frac{2sin4x.cos2x+sin4x}{1+cos2x+2cos^22x-1}=\frac{sin4x\left(2cos2x+1\right)}{cos2x\left(2cos2x+1\right)}=\frac{sin4x}{cos2x}=\frac{2sin2x.cos2x}{cos2x}=2sin2x\)
c/ \(\frac{1+sin2x}{cosx+sinx}-\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}=\frac{sin^2x+cos^2x+2sinx.cosx}{cosx+sinx}-\left(1-tan^2\frac{x}{2}\right)cos^2\frac{x}{2}\)
\(=\frac{\left(sinx+cosx\right)^2}{sinx+cosx}-\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)=sinx+cosx-cosx=sinx\)
d/ \(cos4x+4cos2x+3=2cos^22x-1+4cos2x+3\)
\(=2\left(cos^22x+2cos2x+1\right)=2\left(cos2x+1\right)^2=2\left(2cos^2x-1+1\right)^2=8cos^4x\)
e/
Đúng 0
Bình luận (1)
Giải các phương trình sau:
\(a,cos3x-4cos2x+3cosx-4=0\)
\(b,cos\left(x+\dfrac{\pi}{5}\right).cos\left(x-\dfrac{\pi}{5}\right)=cos\left(\dfrac{2\pi}{5}\right)\)