Bài 1: Cho hình bình hành ABCD. Gọi M, N theo thứ tự là trung điểm của AB, CD; giao điểm của AN và DM là K; giao điểm của BN và CM là L.
1) Chứng minh K, L theo thứ tự là trung điểm của AN và DM, của CM và BN.
2) Chứng minh rằng bốn đường thẳng AC, BD, MN, KL cùng đi qua một điểm.
3) Tứ giác ABCD phải thỏa mãn điều kiện gì để tứ giác MKNL là hình vuông.
DL
Những câu hỏi liên quan
Bài 1 : Cho tứ giác ABCD , gọi M , N, P , Q theo thứ tự là trung điểm của AB , BC , CD , AD . Chứng minh rằng MNPQ là hình bình hành
Xét \(\Delta ABC\), có:
\(\left\{{}\begin{matrix}AM=MB\\AQ=QD\end{matrix}\right.\Rightarrow MQ\) là đường TB của \(\Delta ABC\)
\(\Rightarrow MQ\text{/}\text{/}=\dfrac{1}{2}BD\left(1\right)\)
Xét \(\Delta CBD\), có:
\(\left\{{}\begin{matrix}BN=NC\\CP=PD\end{matrix}\right.\Rightarrow NP\) là đường TB của \(\Delta CBD\)
\(\Rightarrow NP\text{/}\text{/}=\dfrac{1}{2}BD\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow NP\text{/}\text{/}MQ\)
Vậy...............
Đúng 2
Bình luận (0)
Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành.
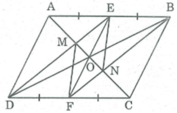
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Chứng minh rằng MNPQ là hình bình hành.
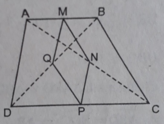
MN // QP (cùng song song với BC)
MN = QP ( =1/2 BC)
⇒ MNPQ là hình bình hành.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E,F theo thứ tự là trung điểm của AB, CD. Gọi M,N theo thứ tự là giao điểm của BD với AF, CE.CM: DM=MN=NB
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AE, CK theo thứ tự tại E, F.
a) CMR: DE=EF=FB
b) Gọi M là trung điểm AD, N trung điểm BC. Chứng minh: tứ giác KMIN là hình bình hành
đầu bài chỗ " đường chéo BD cắt AE" chắc là " đường chéo BD cắt AI" phải không bn???
a) ta có: AB = CD ( ABCD là h.b.h)
=> AK = IC \(\left(=\frac{1}{2}AB=\frac{1}{2}CD\right)\)
mà AK // IC
=> AKCI là hình bình hành ( dấu hiệu)
xét \(\Delta DFC\)
có: DI =IC (gt)
EI // FC ( AKCI là h.b.h)
=> EI là đường trung bình của \(\Delta DFC\)
=> DE = EF ( t/c')
cmtt với \(\Delta AEB\)ta có: EF = FB
=> DE=EF=FB
b) xét \(\Delta ABD\)
có: AM=MD
AK=KB
=> KM là đường trung bình của \(\Delta ABD\)
=> KM // BD và \(KM=\frac{1}{2}BD\)
cmtt với \(\Delta BCD\)ta có: IN//BD và \(IN=\frac{1}{2}BD\)
=> KM // IN (//BD)
\(KM=IN\left(=\frac{1}{2}BD\right)\)
=> KMIN là hình bình hành ( dấu hiệu)
cho hình bình hành abcd .gọi M N theo thứ tự là trung điểm của AB và CD a. chứng minh tứ giác bmdn là hình bình hành b.chứng minh góc amd=góc bnc c gọi i là trung điểm của ac chứng minh m,i,n là thẳng hàng
 a) Do M là trung điểm của AB (gt)
a) Do M là trung điểm của AB (gt)
⇒ BM = AM = AB : 2
Do N là trung điểm của CD (gt)
⇒ CN = DN = CD : 2
Do ABCD là hình bình hành (gt)
⇒ AB = CD và AB // CD
⇒ BM = AB : 2 = CD : 2 = DN
Do AB // CD (cmt)
⇒ BM // DN
Tứ giác BMDN có:
BM // DN (cmt)
BM = DN (cmt)
⇒ BMDN là hình bình hành
b) Do BMDN là hình bình hành (cmt)
⇒ BN // DM
⇒ ∠AMD = ∠MBN (đồng vị) (1)
Do AB // CD (cmt)
⇒ ∠MBN = ∠BNC (so le trong) (2)
Từ (1) và (2) ⇒ ∠AMD = ∠BNC
c) Do ABCD là hình bình hành
I là trung điểm của AC (gt)
⇒ I là trung điểm của BD
Do BMDN là hình bình hành (cmt)
I là trung điểm của BD (cmt)
⇒ I là trung điểm của MN
⇒ M, I, N thẳng hàng
Đúng 1
Bình luận (0)
Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: EMNF là hình bình hành
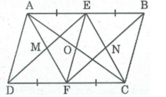
+) Ta có:
AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).
Và AB = CD (tính chất hình bình hành)
Suy ra: AE = CF
+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF
Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành
⇒ AF //CE hay EN // FM (1)
Xét tứ giác BFDE ta có:
AB // CD (gt) hay BE // DF
BE = 1/2 AB (gt)
DF = 1/2 CD (gt)
AB = CD (tính chất hình bình hành)
Suy ra: BE = DF
Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)
Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)
Đúng 0
Bình luận (0)
cho hình bình hành ABCD (với AB>CD) Gọi M và N theo thứ tự là trung điểm của AB và CD A) Chứng minh AN=CM B) Chứng minh tứ giác AMCN là hình bình hành C) Chứng minh AM//CM
Bài 1: Cho hình thang ABCD (AB//CD) có O là giao điểm của AC và BD. Gọi F là trung điểm của CD. E là giao điểm của OF và AB. Chứng minh rằng: E là trung điểm của AB
Bài 2: Cho hình bình hành ABCD, 1 đường thẳng đi qua D cắt AC, AB, CB theo thứ tự ở M, N, K. Chứng minh rằng: a) DM^2 = MN*MK b) DM/DN+DM/DK=1
1:
Xet ΔOAE và ΔOCF có
góc OAE=góc OCF
góc AOE=góc COF
=>ΔOAE đồng dạng với ΔOCF
=>AE/CF=OE/OF
Xét ΔOEB và ΔOFD có
góc OEB=góc OFD
góc EOB=góc FOD
=>ΔOEB đồng dạng với ΔOFD
=>EB/FD=OE/OF=AE/CF
mà CF=DF
nên EB=AE
=>E là trung điểm của BA
Đúng 1
Bình luận (0)
cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:
a) M, N theo thứ tự là trung điểm của CD, AB.
b) EMFN là hình bình hành.




