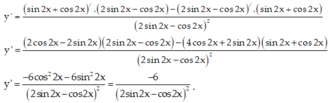Tính đạo hàm của hàm số y= căn cos(x²+2x+3)
LV
Những câu hỏi liên quan
Tính đạo hàm của hàm số y = cos2x . căn bậc hai của ( pi/4 - 2x)
Tính đạo hàm của hàm số sau
y= cos^2021(x căn x)
\(y'=2021\cdot cos\left(x\sqrt{x}\right)^{2020}\cdot\left(cos\left(x\sqrt{x}\right)\right)'\)
\(=2021\cdot\left(-x\sqrt{x}\right)'\cdot sin\left(x\sqrt{x}\right)\cdot cos\left(x\sqrt{x}\right)^{2020}\)
\(=-2021\cdot\dfrac{\left(x^3\right)'}{2\sqrt{x^3}}\cdot sin\left(x\sqrt{x}\right)\cdot cos^{2020}x\sqrt{x}\)
\(=-2021\cdot\dfrac{3x^2}{2x\sqrt{x}}\cdot sin\left(x\sqrt{x}\right)\cdot cos^{2020}x\sqrt{x}\)
\(=-\dfrac{6063}{2}\sqrt{x}\cdot sin\left(x\sqrt{x}\right)\cdot cos^{2020}x\sqrt{x}\)
Đúng 1
Bình luận (1)
Tính đạo hàm của hàm số
y
sin
2
x
+
cos
2
x
2
sin
2
x
-
cos
2
x
A. B. C. D.
Đọc tiếp
Tính đạo hàm của hàm số y = sin 2 x + cos 2 x 2 sin 2 x - cos 2 x
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tính đạo hàm của các hàm số sau:
a) y=\(\dfrac{3x^2-18x-2}{1-2x}-\dfrac{2x-3}{x+4}\)
b) y=\(-\dfrac{\sin x}{3\cos^3x}+\dfrac{4}{3}\tan x\)
Tính đạo hàm của các hàm số sau:
a) \(y = \sin 3x\);
b) \(y = {\cos ^3}2x\);
c) \(y = {\tan ^2}x\);
d) \(y = \cot \left( {4 - {x^2}} \right)\).
a) Đặt \(u = 3{\rm{x}}\) thì \(y = \sin u\). Ta có: \(u{'_x} = {\left( {3{\rm{x}}} \right)^\prime } = 3\) và \(y{'_u} = {\left( {\sin u} \right)^\prime } = \cos u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = \cos u.3 = 3\cos 3{\rm{x}}\).
Vậy \(y' = 3\cos 3{\rm{x}}\).
b) Đặt \(u = \cos 2{\rm{x}}\) thì \(y = {u^3}\). Ta có: \(u{'_x} = {\left( {\cos 2{\rm{x}}} \right)^\prime } = - 2\sin 2{\rm{x}}\) và \(y{'_u} = {\left( {{u^3}} \right)^\prime } = 3{u^2}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 3{u^2}.\left( { - 2\sin 2{\rm{x}}} \right) = 3{\left( {\cos 2{\rm{x}}} \right)^2}.\left( { - 2\sin 2{\rm{x}}} \right) = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
Vậy \(y' = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
c) Đặt \(u = \tan {\rm{x}}\) thì \(y = {u^2}\). Ta có: \(u{'_x} = {\left( {\tan {\rm{x}}} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\) và \(y{'_u} = {\left( {{u^2}} \right)^\prime } = 2u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 2u.\frac{1}{{{{\cos }^2}x}} = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
Vậy \(y' = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
d) Đặt \(u = 4 - {x^2}\) thì \(y = \cot u\). Ta có: \(u{'_x} = {\left( {4 - {x^2}} \right)^\prime } = - 2{\rm{x}}\) và \(y{'_u} = {\left( {\cot u} \right)^\prime } = - \frac{1}{{{{\sin }^2}u}}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = - \frac{1}{{{{\sin }^2}u}}.\left( { - 2{\rm{x}}} \right) = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Vậy \(y' = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Đúng 1
Bình luận (0)
Tính đạo hàm của hàm số y = 2.sin 3x + cos 2x
![]()
![]()
![]()
![]()
Tính đạo hàm cấp hai của mỗi hàm số sau:
a) \(y = 2{x^4} - 3{x^3} + 5{x^2}\)
b) \(y = \frac{2}{{3 - x}}\)
c) \(y = \sin 2x\cos x\)
d) \(y = {e^{ - 2x + 3}}\)
e) \(y = \ln (x + 1)\)
f) \(y = \ln ({e^x} + 1)\)
\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
Đúng 1
Bình luận (0)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)
Đúng 1
Bình luận (0)
e,
\(y = \ln (x + 1) \Rightarrow y' = \frac{1}{{x + 1}} \Rightarrow y'' = - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\)
f,
\(y = \ln ({e^x} + 1) \Rightarrow y' = \frac{{{e^x}}}{{{e^x} + 1}} \Rightarrow y'' = - \frac{{{e^x}.{e^x}}}{{{{\left( {{e^x} + 1} \right)}^2}}} = - \frac{{{e^{2x}}}}{{{{\left( {{e^x} + 1} \right)}^2}}}\)
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số \(y = 2\cos \left( {\frac{\pi }{4} - 2x} \right).\)
\(y'=-2\left(\dfrac{\pi}{4}-2x\right)'sin\left(\dfrac{\pi}{4}-2x\right)\\ =4sin\left(\dfrac{\pi}{4}-2x\right)\)
Đúng 0
Bình luận (0)