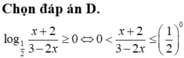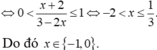Có bao nhiêu số nguyên x thỏa mãn | 2x - 2| + | 2x - 6| < 4
NV
Những câu hỏi liên quan
Có bao nhiêu số nguyên tố thỏa mãn | 2x - 2| + | 2x - 6| < 4
x=2=>2+2=4 ko thao man <4
x=3=>4+0=4 ko thoa man <4
x>3 VT>4 => ko co so nao thoa man dau bai
Đúng 0
Bình luận (0)
khong co so nao thoa man dau bai dau nhe
Đúng 0
Bình luận (0)
Có bao nhiêu số x thỏa mãn : |2x-2| + |2x-6| = 4
Có bao nhiêu số x thỏa mãn : |2x-2| + |2x-6| = 4
|2x - 2| + |2x - 6| = |2x - 2| + |6 - 2x| = 4
Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)ta có:
\(\left|2x-2\right|+\left|6-2x\right|\ge\left|2x-2+6-2x\right|=\left|4\right|=4\)
Mà theo đề bài: |2x - 2| + |6 - 2x| = 4 nên \(\hept{\begin{cases}2x-2\ge0\\2x-6\le0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}2x\ge2\\2x\le6\end{cases}}\)\(\Rightarrow2\le2x\le6\)\(\Rightarrow1\le x\le3\)
Vậy có vô số số x thỏa mãn đề bài (nếu số x nguyên thì chỉ có 3 số thôi)
Đúng 0
Bình luận (0)
Có bao nhiêu số x thỏa mãn : |2x-2| + |2x-6| = 4
có bao nhiêu số nguyên x thỏa mãn điều kiện 2x+20⋮(x+6)
2x + 20 \(⋮\) x + 6
2( x + 10) \(⋮\) x + 6
x + 10 \(⋮\) x + 6
x + 6 + 4 \(⋮\) x + 6
4 \(⋮\) x + 6
x + 6 = -4 => x = -10
x + 6 = - 2=> x = -8
x + 6 = - 1=> x = -7
x + 6 = 1 => x -5
x + 6 = 2 => x = -4
x + 6 = 4 => x = -2
vậy x \(\in\) { -10; -8; -7; -5; -4; -2; }
Đúng 1
Bình luận (0)
Có bao nhiêu số nguyên x thỏa mãn : \(\left|2x-2\right|+\left|2x-6\right|< 4\)
a) 3
b) 0
c) 2
d) 1
Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(\left|2x-2\right|+\left|2x-6\right|=\left|2x-2\right|+\left|6-2x\right|\ge\left|2x-2+6-2x\right|=\left|4\right|=4\)
Do đó, |2x - 2| + |2x - 6| < 4 là vô lý
Vậy không tồn tại giá trị x nguyên thỏa mãn đề bài
Đúng 0
Bình luận (0)
có bao nhiêu số nguyên thỏa mãn |2x-2|+|2x-6|<4
(giải chi tiết giup mk nhé mk đang rất gấp)
có bao nhiêu số nguyên \(x\) thỏa mãn \(x^4-2x^2=0\)
chọn câu trả lời đúng nhất :
| 3 | 1 | 0 | 2 |
\(x^2\left(x^2-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy có 3 số nguyên t/m
Đúng 3
Bình luận (0)
cho hình chữ nhật ABCD. Góc nào sau đây có số đo bằng góc ACD
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên x thỏa mãn bất phương trình
log
1
/
2
x
+
2
3
-
2
x
≥
0...
Đọc tiếp
Có bao nhiêu số nguyên x thỏa mãn bất phương trình log 1 / 2 x + 2 3 - 2 x ≥ 0 ?
A. 3
B. 0.
C. 1.
D. 2.