Cho tam giác ABC vuông tại A có góc B=30o và BC = a. Tính AC theo a.
PT
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có góc ACB = 30o. Tia phân giác của góc B cắt AC tại M. Trên cạnh BC lấy điểm E sao cho BE = BA.
a) Chứng minh : ME vuông góc với BC
b) Tam giác AEB và AEC là tam giác gì? Vì sao?
c) Kẻ CH vuông góc với BM. CH cắt AB tại F. Chứng minh 3 điểm E, M, F thẳng hàng
a) Xét ΔAMB và ΔEMB có
BA=BE(gt)
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
BM chung
Do đó: ΔAMB=ΔEMB(c-g-c)
Suy ra: \(\widehat{MAB}=\widehat{MEB}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{MEB}=90^0\)
hay ME\(\perp\)BC(đpcm)
b) Ta có: ΔABC vuông tại A(gt)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}+30^0=90^0\)
\(\Leftrightarrow\widehat{ABC}=60^0\)
hay \(\widehat{ABE}=60^0\)
Xét ΔABE có BA=BE(gt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Xét ΔBAE cân tại B có \(\widehat{ABE}=60^0\)(cmt)
nên ΔBAE đều(Dấu hiệu nhận biết tam giác đều)
Đúng 2
Bình luận (0)
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC a góc
B
C
A
^
60
o
Góc giữa B’C và mặt phẳng (AA’C’C) bằng
30
o...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a góc B C A ^ = 60 o Góc giữa B’C và mặt phẳng (AA’C’C) bằng 30 o Tính theo a, độ dài AC'
A. AC' = a
B. AC' = 3a
C. AC' = a 3
D. AC' = 3 a 3
Đáp án B
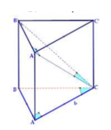
Ta có

Đồng thời
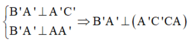
Nên
![]()
Tam giác B'A'C vuông tại A' có
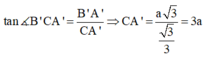
![]()
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AC 6 cm, góc ACB bằng 30o. Vẽ (O) đường kính AC cắt BC tại D, dây DE vuông góc với AC tại Ha) Tính BC.b) Chứng minh CDE là tam giác đều.c) Qua B vẽ đường thẳng tiếp xúc với (O) tại M. Chứng minh BDM và BMC đồng dạng.d) Gọi K là hình chiếu vuông góc của H lên EC và I là trung điểm HK. Chứng minh: DK vuông góc với CI.
Đọc tiếp
Cho tam giác ABC vuông tại A, có AC= 6 cm, góc ACB bằng 30o. Vẽ (O) đường kính AC cắt BC tại D, dây DE vuông góc với AC tại H
a) Tính BC.
b) Chứng minh CDE là tam giác đều.
c) Qua B vẽ đường thẳng tiếp xúc với (O) tại M. Chứng minh BDM và BMC đồng dạng.
d) Gọi K là hình chiếu vuông góc của H lên EC và I là trung điểm HK. Chứng minh: DK vuông góc với CI.
a: \(BC=AC:\sin B=6:\sin60^0=4\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có gốc B = 30o, BC = 18cm. Tính AC?
\(AC=\sin B\cdot BC=\dfrac{1}{2}\cdot18=9\left(cm\right)\)
Đúng 2
Bình luận (0)
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(ADH)
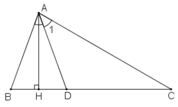
Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o
Đúng 0
Bình luận (0)
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(HAD)
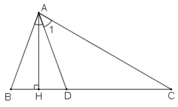
ΔADH vuông tại H nên:
∠(HAD) + ∠(ADH) = 90o (tính chất tam giác vuông)
⇒∠ (HAD) = 90o-∠(ADH)o = 90o - 70o = 20o
Đúng 0
Bình luận (0)
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(BAC)
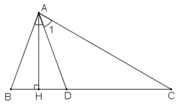
Trong ΔABC có:
∠(BAC) + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Mà ∠(BAC) + 70o + 30o = 180
Vậy ∠(BAC) = 180o-70o - 30o = 80o
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, biết \(tgB=\frac{4}{3}\)và BC = 10. Tính AB, AC.
Bài 2: Cho tam giác ABC cân tại A, AB=AC=17, BC=16. Tính đường cao AH và góc A, góc B của tam giác ABC.
Bài 3: Cho tam giác ABC có \(\widehat{B}=60\) ,các hình chiếu vuông góc của AB và AC lên BC theo thứ tự bằng 12 và 18. Tính các góc và đường cao của tam giác ABC.
Cho tam giác ABC vuông tại A có AC=3cm, AB=4cm, BC=5cm. a)Chứng minh tam giác ABC vuông. Tính góc B và C b) Phân giác của góc A cắt BC tại D. Tính BD và CD.
a) Xét ΔABC có
\(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}\simeq53^0\)
\(\Leftrightarrow\widehat{B}=37^0\)
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{4}=\dfrac{CD}{3}\)
mà BD+CD=5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{CD}{3}=\dfrac{BD+CD}{4+3}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{20}{7}cm;CD=\dfrac{15}{7}cm\)
Đúng 0
Bình luận (0)



