Cho tứ giác ABCD có góc B + góc D = 90 độ
Chứng minh AB2.CD2 + AD2.BD2 = AC2.BD2
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho tứ diện ABCD có trọng tâm G. Chứng minh AB2 + AC2 + AD2 + BC2 + BD2 + CD2 = 4(GA2 + GB2 + GC2 + GD2)
Cho hình bình hành ABCD. CM: AB2 + BC2 + CD2 +DA2 = AC2 +BD2
Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)
Hôm nay 20/11 nma e vẫn phải làm bài tập:((, mn giúp em với hic
Cho hình bình hành ABCD. Chứng minh rầng: AC2 +BD2=2(AB2+AD2)
Cho tứ giác ABCD có AB=AB=BC, biết góc A + góc C =180 độ.
a, Chứng minh DB là tia phân giác góc D
b, Tứ giác ABCD là hình gì?
Cho tứ giác ABCD có O là giao điểm các tia phân giác của các góc C và D.
a) Tính góc COD biết góc A= 120°, góc B= 90°
b) Tính góc COD theo góc A và góc B
c) Các tia phân giác của góc A và B cắt nhau ở I và cắt các tia phân giác các góc C và D thứ tự ở E và F. C/m tứ giác OEIF có các góc đối bù nhau
a) Ta có: \(\widehat{B}=120^o,\widehat{A}=90^o\Rightarrow\widehat{C}+\widehat{D}=360^o-\widehat{A}-\widehat{B}=150^o\)
CO, DO là hai tia phân giác góc C và góc D
=> \(\widehat{C_1}+\widehat{D_1}=\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}=\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)=\frac{1}{2}.150^o=75^o\)
=> \(\widehat{COD}=180^o-\left(\widehat{C_1}+\widehat{D_1}\right)=180^o-75^o=105^o\)
b)
Xét tam giác COD
Ta có: \(\widehat{COD}=180^o-\left(\widehat{C_1}+\widehat{D_1}\right)=180^o-\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)\)
Vì: \(\widehat{C_1}+\widehat{D_1}=\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}=\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)\)
Mặt khác: Xét tứ giác ABCD ta có: \(\widehat{C}+\widehat{D}=360^o-\widehat{A}-\widehat{B}\)
=> \(\widehat{COD}=180^o-\frac{1}{2}\left(360^o-\widehat{A}-\widehat{B}\right)=\frac{1}{2}\widehat{A}+\frac{1}{2}\widehat{B}\)
c) Tương tự ta cũng chứng minh dc:
\(\widehat{BIA}=\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}\)
=> \(\widehat{COD}+\widehat{BIA}=\frac{1}{2}\widehat{A}+\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}=\frac{1}{2}\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)=\frac{1}{2}.360^o=180^o\)
=>\(\widehat{FOE}+\widehat{EIF}=180^o\)
=> \(\widehat{OEI}+\widehat{IFO}=180^o\)
Vậy tứ giác EIF có các góc đối bù nhau!
Ta có BAD + ABC + BCD + CDA = 360 độ
ADC + BCD = 360 - 120 - 90 = 150 độ
=> BCO = OCD = 1/2 BCD
=> ADO = ODC = 1/2 ADC
=> ODC + OCD = 1/2 ODC + 1/2 OCD = ODC+OCD/2
=> ODC + OCD = 150 /2 =75 độ
Mà ODC + OCD +DOC = 180 độ
=> DOC = 180 - 75 = 105 độ
B) COD = 180 - (ODC + OCD)
=> COD = 180 - 1/2ADC + 1/2 BCD
Mà ADC + BCD = 360 - ( BAD + ABC)
COD = 180 - [ 360 - 1/2(BAD + ABC )]
Cho tứ giác ABCD có AB=AB=BC, biết góc A + góc C =180 độ.
a, Chứng minh DB là tia phân giác góc D
b, Tứ giác ABCD là hình gì?
a: Xét tứ giác ABCD có \(\widehat{BAD}+\widehat{BCD}=180^0\)
nên ABCD là tứ giác nội tiếp
Xét đường tròn ngoại tiếp tứ giác ABCD có
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB
\(\widehat{CDB}\) là góc nội tiếp chắn cung CB
mà \(sđ\stackrel\frown{AB}=sđ\stackrel\frown{CB}\)
nên \(\widehat{ADB}=\widehat{CDB}\)
hay DB là tia phân giác của góc ADC
b: Xét ΔABD có AB=AD
nên ΔABD cân tại A
=>\(\widehat{ABD}=\widehat{ADB}\)
=>\(\widehat{ABD}=\widehat{BDC}\)
hay AB//CD
=>ABCD là hình thang
mà ABCD là tứ giác nội tiếp
nên ABCD là hình thang cân
Tứ giác abcd có góc A=góc D=90°. Phân giác góc C cắt AD tại trung điểm M. Kẻ ME vuông góc với BC. Tính góc AED.
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi A C 2 + B D 2 = A D 2 + B C 2
Giả sử AB ⊥ CD ta phải chứng minh:
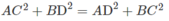
Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
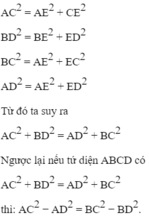
Nếu
A
C
2
−
A
D
2
=
B
C
2
−
B
D
2
=
k
2
thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho 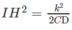
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.
Nếu A C 2 − A D 2 = B C 2 − B D 2 = - k 2 thì ta có và đưa về trường hợp xét như trên A C 2 − A D 2 = B C 2 − B D 2 = - k 2 .
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi A B 2 + C D 2 = A C 2 + B C 2 .
Cho tứ giác ABCD có góc B= góc D. Góc C= alpha (alpha <90 độ.) Trên nửa mặt phẳng bờ BD không chứa C lấy điểm E sao cho góc ABE= góc ABD và góc ADE= góc ADB. Tính góc BED theo alpha
BÀI 1: a) CHO HÌNH BÌNH HÀNH ABCD CÓ góc >90 . SO SÁNH AC VÀ BD
b) TỨ GIÁC ABCD CÓ \hat{A} , \hat{B} ,\hat{C} TÙ. CHỨNG MINH AC<BD
BÀI 2: CHO HÌNH CHỮ NHẬT ABCD. KẺ BH VUÔNG GÓC AC (H THUỘC AC). TRÊN TIA ĐỐI CỦA TIA BH LẤY ĐIỂM E SAO CHO BE = AC. CHỨNG MINH RẰNG GÓC ADE = 45 ĐỘ
BÀI 3 : CHỨNG MINH RẰNG TỨ GIÁC CÓ GIAO ĐIỂM HAI ĐƯỜNG CHÉO TRÙNG VỚI GIAO ĐIỂM CÁC ĐOẠN THẲNG NỐI TRUNG ĐIỂM CÁC CẠNH ĐỐI DIỆN THÌ TỨ GIÁC ĐÓ LÀ HÌNH BÌNH HÀNH
BÀI 4: CHO TAM GIÁC ABC VUÔNG TẠI A ( AC > AB), ĐƯỜNG CAO AH. TRÊN TIA HC LẤY HD = HA, ĐƯỜNG VUÔNG GÓC VỚI BC TẠI D CẮT AC TẠI E.
a) CHỨNG MINH AE = AB
b) GỌI M LÀ TRUNG ĐIỂM BE . TÍNH GÓC AHM
BÀI 5: TỨ GIÁC ABCD CÓ CÓ GÓC A = GÓC B =90 ĐỘ VÀ AC = BD.
a) ABCD CÓ PHẢI LÀ HÌNH CHỮ NHẬT KHÔNG? C/M
b) LẤY ĐIỂM M NẰM GIỮA A,C. VẼ MK VUÔNG GÓC AB TẠI K , MH VUÔNG GÓC AD TẠI H. CHỨNG MINH HK // BD
C) TIA MH CẮT BC Ở E, TIA KM CẮT CD TẠI F. MD CẮT HF Ở I, MB CẮT KE TẠI J/ CHỨNG MINH HK + EF = 2IJ
đc có tí điểm bắt lm 5 câu dài ko ai muốn lm