Cho hình chữ nhật ABCD có AB = 8 cm; BC = 6 cm. Vẽ đường cao AH của tam giác ADB.
a) Chứng minh Tam giác AHB đồng dạng với tam giác BCD.
b) Tính độ dài đoạn thẳng AH .
c) Tính diện tích tam giác AHB
cho hình chữ nhật ABCD có đường chéo DB = 68 cm và AD phần AB bằng 8 phần 15 . tính độ dài các cạnh của hình chữ nhật
Ta có: \(\dfrac{AD}{AB}=\dfrac{8}{15}\)
nên \(AD=\dfrac{8}{15}AB\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow\left(\dfrac{8}{15}AB\right)^2+AB^2=68^2=4624\)
\(\Leftrightarrow AB^2\cdot\dfrac{289}{225}=4624\)
\(\Leftrightarrow AB^2=3600\)
\(\Leftrightarrow AB=60\left(cm\right)\)
\(\Leftrightarrow AD=\dfrac{8}{15}AB=\dfrac{8}{15}\cdot60=32\left(cm\right)\)
\(\Leftrightarrow CD=60cm;BC=32cm\)
cho hình chữ nhật ABCD có đường chéo DB = 68 cm và AD phần AB bằng 8 phần 5 . tính độ dài các cạnh của hình chữ nhật
Cho hình chữ nhật ABCD có AB = 3 (cm), AD = 5 (cm). Thể tích khối trụ hình thành được khi quay hình chữ nhật ABCD quanh đoạn AB bằng
A. 25 π ( cm 3 )
B. 75 π ( cm 3 )
C. 50 π ( cm 3 )
D. 45 π ( cm 3 )
Cho hình hộp chữ nhật ABCD. EFGH (Hình 4) có AD = 8 cm, DC = 5 cm, DH = 6,5 cm. Tìm độ dài các cạnh AB, FG, AE.
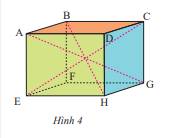
Ta có: AB = DC = EF = HG, mà DC = 5 cm nên AB = 5 cm
AD = BC = FG = EH, mà AD = 8 cm nên FG = 8 cm
AE = FB = DH = CG, mà DH = 6,5 cm nên AE = 6,5 cm
1,Cho hình chữ nhật ABCD, biết AB = 8 cm, BC = 6 cm. Vẽ đường cao AH của ∆ADB. Khi đó tỉ số diện tích ∆ADB và ∆HDA
2,Cho hình chữ nhật ABCD, biết AB = 8 cm, BC = 6 cm. Vẽ đường cao AH của ∆ADB. Khi đó độ dài của đoạn thẳng BH là
Bài 1:
Xét tam giác $DHA$ và $DAB$ có:
$\widehat{D}$ chung
$\widehat{DHA}=\widehat{DAB}=90^0$
$\Rightarrow \triangle DHA\sim \triangle DAB$ (g.g)
$\Rightarrow \frac{DH}{DA}=\frac{DA}{DB}\Rightarrow DA^2=DH.DB(1)$
Tương tự: $\triangle BHA\sim \triangle BAD$ (g.g)
$\Rightarrow \frac{BH}{BA}=\frac{BA}{BD}\Rightarrow AB^2=BH.BD(2)$
Từ $(1);(2)\Rightarrow (\frac{AD}{AB})^2=\frac{DH}{BH}$
$\Rightarrow \frac{DH}{BH}=(\frac{6}{8})^2=\frac{9}{16}$
$\Rightarrow \frac{DH}{BD}=\frac{9}{25}$
\(\frac{S_{ADB}}{S_{HDA}}=\frac{AH.BD}{AH.HD}=\frac{BD}{HD}=\frac{25}{9}\)
Bài 2:
Theo kết quả bài 1, ta có $\frac{DH}{DB}=\frac{9}{25}$
Mà $DB=\sqrt{AB^2+AD^2}=\sqrt{8^2+6^2}=10$ (cm) theo định lý Pitago
$\Rightarrow DH=\frac{9}{25}.DB=\frac{9}{25}.10=3,6$ (cm)
$BH=BD-DH=10-3,6=6,4$ (cm)
Trong Hình 94, hình chữ nhật ABCD có AB = 9 cm, AD = 6 cm; hình chữ nhật A’B’C’D’ có A’B’ = 3 cm, A’D’ = 2 cm; hình chữ nhật A’’B’’C’’D’’ có A’’B’’ = 3 cm, A’’D’’ = 2 cm. Quan sát Hình 94 và cho biết:
a) Hai hình chữ nhật A’’B’’C’’D’’, ABCD có đồng dạng phối cảnh hay không.
b) Hai hình chữ nhật A’B’C’D’, A’’B’’C’’D’’ có bằng nhau hay không.
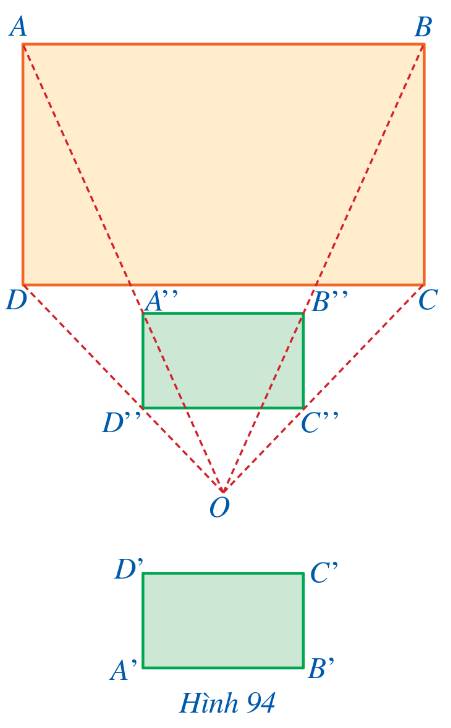
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau
Màn hình điện thoại có hình dạng chữ nhật ABCD biết AB=8 cm; BC=6 cm hỏi AC=?
áp dụng đ/lí py-ta-go vào ΔABC, ta có:
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}\Leftrightarrow AC=\sqrt{8^2+6^2}=10\left(cm\right)\)
`AC` là đường chéo hình chữ nhật
Ta có: `AB^2 + BC^2 = AC^2`
`=> 64 + 36 = AC^2`
`=> AC = sqrt 100 = 10`.
cho hình chữ nhật ABCD có AB=2 dm , 12 cm. chu vi hình chữ nhật ABCD là ;
Đổi: \(2dm=20cm\)
Chu vi hình chữ nhật là:
\(\left(20+12\right)\cdot2=64\left(cm\right)\)
Vậy chu vi của hình chữ nhật là \(64cm\)
2dm=20 cm
chu vi HCN là :
[ 20+12] . 2 =64
tính diện tích hình tứ giác AECG . biết hình chữ nhật ABCD có AD = 20 cm ; AB = 14 cm ; BE = 8 cm và DG = 9 cm.
tính diện tích hình tứ giác AECG . biết hình chữ nhật ABCD có AD = 20 cm ; AB = 14 cm ; BE = 8 cm và DG = 9 cm.
diện tích hình chữ nhật : chiều dai nhân chiều rộng là 20.14=280
diện tích tứ giác vẫn là chiều dài nhân với chiều rộng là:8.9=72