tìm khoảng đơn điệu của hàm số y=|x^2-4x+3|+4x+3
BT
Những câu hỏi liên quan
Cho hàm số \(y=\sqrt{x^2-4x+2}\)Tìm khoảng đơn điệu của hàm số
Tìm các khoảng đơn điệu của hàm số sau \(y=\dfrac{x+2}{\sqrt{x^2-x+3}}\)
TXĐ: \(D=R\)
\(y'=\dfrac{-5x+8}{2\sqrt{\left(x^2-x+3\right)^3}}=0\Rightarrow x=\dfrac{8}{5}\)
Dấu của y' trên trục số:
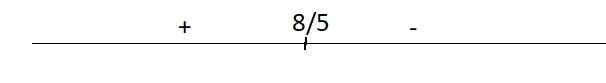
Từ đây ta thấy hàm đồng biến trên \(\left(-\infty;\dfrac{8}{5}\right)\) và nghịch biến trên \(\left(\dfrac{8}{5};+\infty\right)\)
Đúng 1
Bình luận (1)
Tìm các khoảng đơn điệu của hàm số y=x²+2x+2/x+1
Tìm các khoảng đơn điệu của các hàm số sau:
\(y=x^2+\left|x^2-7x+10\right|\)
Lời giải:
Với $x\in (5;+\infty)\cup (-\infty;2)$ thì:
$y=x^2+x^2-7x+10=2x^2-7x+10$
$y'=4x-7=0\Leftrightarrow x=\frac{7}{4}$ (không nằm trong khoảng đang xét)
Với $x\in [2;5]$ thì:
$y=x^2-(x^2-7x+10)=7x-10$
$y'=7>0$
Lập BBT ta thấy:
Hàm $y$ đồng biến trên trên $(2;+\infty)$ và nghịch biến trên $(-\infty;2)$
Đúng 1
Bình luận (0)
Tìm khoảng đơn điệu của hàm số:
1, \(y=x^2-2\left|x\right|-3\)
2, \(y=sin\left(2x\right)-cos\left(2x\right)+3x\)
Mọi người giúp mình với ạ!! Mình cảm ơn nhiều!!!
Tìm các khoảng đơn điệu của hàm số y=|-x|
giải hệ phương trình bằng ứng dụng tính đơn điệu của hàm số : \(\hept{\begin{cases}x^3+x^2+x+1=4y\\y^3+y^2+y+1=4z\\z^3+z^2+z+1=4x\end{cases}}\)
Giả sử \(x\ge y\ge z\)cũng được mà.
Tìm các khoảng đơn điệu của các hàm số: y = 3 x + 1 1 - x
Tập xác định: D = R \ {1}
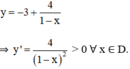
y' không xác định tại x = 1
Bảng biến thiên:
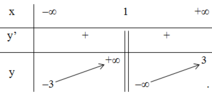
Vậy hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)
Đúng 0
Bình luận (0)
Tìm các khoảng đơn điệu của các hàm số: y = x 2 - x - 20
Tập xác định: D = (-∞ ; -4] ∪ [5; +∞)
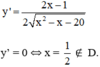
y' không xác định tại x = -4 và x = 5
Bảng biến thiên:

Vậy hàm số nghịch biến trong khoảng (-∞; -4); đồng biến trong khoảng (5; +∞).
Đúng 0
Bình luận (0)


