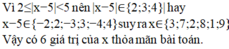Có bao nhiêu số nguyên x thỏa mãn | x - 1| + | x - 5| = 4
NV
Những câu hỏi liên quan
Có bao nhiêu số nguyên x thỏa mãn | x-1| + | x - 5| = 4
TH1 : x > 1
|x-1| + |x-5| = 4
-x+1 - x + 5 = 4
-2x = -2
x = 1
TH2 : 1 < hoặc = x < 5
|x-1| + |x-5| = 4
x - 1 - x + 5 = 4
4 = 4 ( thỏa mãn vs mọi x )
TH2 : x > hoặc = 5
|x-1| + |x-5| = 4
x - 1 + x - 5 = 4
2x = 10
x = 5
Đúng 1
Bình luận (0)
\(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\ge\left|x-1+5-x\right|=4\)
Dấu = xảy ra khi \(1\le x\le5\)
Vậy có 5 số
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Có bao nhiêu số nguyên X thỏa mãn \(\left|x-1\right|+\left|x-5\right|=4\)
Xét vế trái ta có:
/x-1/+/x-5/=/x-1/+/5-x/\(\ge\)/x-1+5-x/=4
Mà vế phải là 4
\(\Rightarrow\)/x-1/+/x-5/=4\(\Leftrightarrow\left(x-1\right)\left(5-x\right)>0\)
Sau đó bạn xét 2 trường hợp
Th1:(x-1)>0 và (5-x)>0
Th2:(x-1)<0 và (5-x)<0
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên X thỏa mãn \(\left|x-1\right|+\left|x-5\right|=4\)
Có: \(\left|x-1\right|\ge x-1\); \(\left|x-5\right|\ge5-x\forall x\)
\(\Rightarrow\left|x-1\right|+\left|x-5\right|\ge\left(x-1\right)+\left(5-x\right)=4\)
Mà theo đề bài, |x - 1| + |x - 5| = 4
\(\Rightarrow\begin{cases}x-1\ge0\\x-5\le0\end{cases}\)\(\Rightarrow\begin{cases}x\ge1\\x\le5\end{cases}\)\(\Rightarrow1\le x\le5\)
Mà x nguyên \(\Rightarrow x\in\left\{1;2;3;4;5\right\}\)
Vậy có 5 số nguyên x thỏa mãn đề bài
Đúng 0
Bình luận (0)
có bao nhiêu số nguyên x thỏa mãn điều kiện 9,5<x<17,7
có bao nhiêu số nguyên x thỏa mãn -1,23<x<2,5
a: Ta có: 9,5<x<17,7
mà x là số nguyên
nên \(x\in\left\{10;11;12;...;17\right\}\)
Số số hạng thỏa mãn là 17-10+1=8(số)
b: Ta có: -1,23<x<2,5
mà x là số nguyên
nên \(x\in\left\{-1;0;1;2\right\}\)
=>Có 4 số thỏa mãn
Đúng 2
Bình luận (1)
Có bao nhiêu số nguyên x thỏa mãn : I X-1 I + I X-5 I = 4
Giải chi tiết giúp mình nha
Với bài này, ta phải chia trường hợp để phá ngoặc. VD để |x-1| = x-1 thì x-1 phải lớn hơn hoặc bằng 0, hay x lớn hơn hoặc bằng 1 là 1 trường hợp. Còn nếu x nhỏ hơn 1 thì |x-1| = -(x-1)
TH1: \(x< 1\), ta có :
\(-\left(x-1\right)+\left[-\left(x-5\right)\right]=4\)
\(1-x+5-x=4\)
\(6-2x=4\)
\(x=\frac{6-4}{2}=1\)( Không thỏa mãn x < 1 )
TH2 \(1\le x\le5;\)ta có :
\(\left(x-1\right)+\left[-\left(x-5\right)\right]=4\)
\(\Rightarrow x-1+5-x=4\)
\(4=4\)( Thỏa mãn )
Do đó với \(1\le x\le5;\) thì đẳng thức luôn thỏa mãn
TH3 : \(x>5;\)có :
\(x-1+x-5=4\)
\(2x-6=4\)
\(x=\frac{6+4}{2}=5\)(Không thỏa mãn )
Vậy \(1\le x\le5.\)
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên x thỏa mãn: (-3)x(-2)? A. 3 . B. 5 . C. 4. D. 3 .
Đọc tiếp
Có bao nhiêu số nguyên x thỏa mãn: (-3)<x<(-2)? A. 3 . B. 5 . C. 4. D. 3 .
Xem thêm câu trả lời
Có bao nhiêu số nguyên x thỏa mãn x+4 chia hết cho x+1
x+1 chia hết cho x+1
=> 4 chia hết cho x+1
=> x+1 \(\in\) Ư(4) = { -2 ; -1 ; 1 ; 2 }
| x+1 | -2 | -1 | 1 | 2 |
| x | -3 | -2 | 0 | 1 |
Vậy x\(\in\) { -3 ; -2 ; 0 ; 1 }
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên x thỏa mãn 2≤|x−5|<5?
A. 3
B. 2
C. 6
D. 4
Có bao nhieu số nguyên x thỏa mãn | x - 1| + | x - 5| = 4
Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\ge\left|x-1+5-x\right|=\left|4\right|=4\)
Theo đề bài lại có: |x - 1| + |x - 5| = 4 nên \(\begin{cases}x-1\ge0\\x-5\le0\end{cases}\)\(\Rightarrow\begin{cases}x\ge1\\x\le5\end{cases}\)
Mà x nguyên nên \(x\in\left\{1;2;3;4;5\right\}\)
Vậy có 5 số nguyên thỏa mãn đề bài
Đúng 0
Bình luận (0)