tam giác ABC cân tại A. Đường cao AH; trên tia đối của tia AH lấy D sao cho HD = HA. Trên tia đối của tia CB lấy E sao cho CE = CB
Chứng minh: a/ C là trọng tâm tam giác ADE
b/ AC cắt DE tại M. Chứng minh AE // HM
Cho tam giác ABC. Chứng minh rằng:
a) Nếu đường cao AH đồng thời là đường trung tuyến thì tam giác ABC cân tại A.
b) Nếu tam giác ABC cân tại A thì đường trung tuyến AH cũng là đường cao.
mình hong bik làm
Cho tam giác ABC cân tại A, đường cao AH và trung tuyến BK cắt nhau tại G. Tia CG cắt AB tại I
Cho tam giác ABC cân tại A; đường cao AH và trung tuyến BK cắt nhau tại G. Tia CG cắt AB tại I
a, Chứng minh tam giác AIG = tam giác AKG
b, Biết AH = 18 cm, BC = 16cm. Tính độ dài đoạn thẳng GI
c, Chứng minh IK // BC
Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
Cho tam giác ABC cân tại A, có đường cao AH = 32 cm, đường cao BK = 38,4 cm.
a) tính các cạnh của tam giác ABC. b) đường trung trực của AC cắt AH tại O, tính OH GIÚP MÌNH VS ẠCho tam giác ABC cân tại A có đường cao AH. Phân giác trong của góc B cắt AH tại I. Biết AB = 10cm, AI/AH = 4/5. Chu vi tam giác ABC
\(\dfrac{AI}{AH}=\dfrac{4}{5}\)
=>\(AI=\dfrac{4}{5}AH\)
Ta có: AI+HI=AH
=>\(HI=AH-AI=AH-\dfrac{4}{5}AH=\dfrac{1}{5}AH\)
\(\dfrac{AI}{IH}=\dfrac{\dfrac{4}{5}AH}{\dfrac{1}{5}AH}=\dfrac{4}{5}:\dfrac{1}{5}=4\)
Xét ΔBAH có BI là phân giác
nên \(\dfrac{BA}{BH}=\dfrac{AI}{IH}\)
=>\(\dfrac{10}{BH}=4\)
=>BH=10/4=2,5(cm)
ΔABC cân tại A có AH là đường cao
nên H là trung điểm của BC
=>\(BC=2\cdot BH=5\left(cm\right)\)
Chu vi tam giác ABC là:
10+10+5=25(cm)
Cho tam giác ABC có đường cao AH đồng thời là đường phân giác của góc A Chúng minh tam giác ABC cân tại A.
cho tam giác ABC cân tại A , vẽ trung tuyến AH . chứng minh rằng AH cũng là phân giác , đường cao, đường trung tuyến của tam giác ABC
Cho tam giác ABC cân tại A, đường cao AH
a, chứng minh: tam giác ABH = tam giác ACH
b, chứng minh: AH là đường phân giác của tam giác ABC
c, chứng minh: AH là đường trung trực của tam giác ABC
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABH` và `\Delta ACH`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao của} \Delta ABC)$
`=> \Delta ABH = \Delta ACH (ch-gn)`
`b,`
Vì `\Delta ABH = \Delta ACH (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 cạnh tương ứng})$
`-> \text {AH là đường phân giác của}` `\Delta ABC`
`c,`
Vì `\Delta ABH = \Delta ACH (a)`
`-> \text {HB = HC}`
Ta có:
`\text {AH} \bot \text {BC}`
`\text {HB = HC}`
`-> \text {AH là đường trung trực của}` `\Delta ABC`.
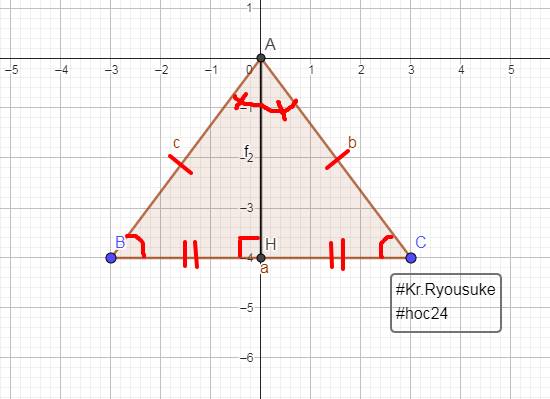
Cho tam giác ABC cân tại A, có đường cao AH. Biết AH = 12cm, BC = 10cm. Tính chu vi tam giác ABC.
Ta có :
AC=AB=10cm (tg cân )
Tính: BC
Có : AC+AB=BC
=> 10+10=BC
=> 20 =BC
Chu vi hình tam giác ABC là :
10+10+20=40 cm
ta có:
AC=AB=10cm(tg cân)
Tính BC
Có: AC+AB=BC
=>10+10=BC
=>20=BC
Chu vi hình tam giác ABC là:10+10=20=40 cm
Đáp số:40cm
Cho tam giác ABC cân tại A, đường cao AH (h.55). Tìm hình đối xứng với mỗi cạnh của tam giác ABC qua AH.
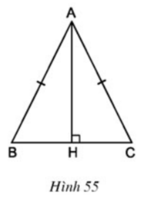
AB đối xứng với AC qua AH BC đối xứng với CB qua AH
Cho tam giác ABC cân tại A; các đường cao AH,BK.Tính diện tích tam giác ABC biết AH=5cm,NK=6cm