Mọi người giải dùm em câu 38 với ạ 👉👈
DY
Những câu hỏi liên quan
Giúp mình câu hình với . Mình cần gấp ạ . Cảm ơn mọi người nhiều 👉👈
Câu I:
1) Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}+2}{\sqrt{x}}-\dfrac{x+\sqrt{x}-4}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{x+\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x+x+\sqrt{x}-2-x-\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{x+2}{\sqrt{x}}\)
2) Để P=3 thì \(\dfrac{x+2}{\sqrt{x}}=3\)
\(\Leftrightarrow x+2=3\sqrt{x}\)
\(\Leftrightarrow x-3\sqrt{x}+2=0\)
\(\Leftrightarrow x-\sqrt{x}-2\sqrt{x}+2=0\)
\(\Leftrightarrow\sqrt{x}\cdot\left(\sqrt{x}-1\right)-2\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=1\left(loại\right)\end{matrix}\right.\)
Vậy: Để P=3 thì x=4
Đúng 0
Bình luận (0)
Mọi người giúp mk với 😓👉👈
III,
1. different
2. between
3. out
4. well
5. downstairs
6. written
7. has lived
8. as cold as
9. to study
10. taking
11. have to
12. between
13. himself
14. How long
15. on
IV,
1. My family used to visit Sa Pa last summer vacation.
2. They used to go to school by bus last year.
3. Na isn’t as beautiful as Trang.
4. French is more difficult than English.
5. They have lived here for 10 years.
6. She enjoys swimming and outdoor activities.
Đúng 1
Bình luận (0)
giúp mình(em) với ạ ((👉👈
Đọc tiếp
giúp mình(em) với ạ =((
a: =(-3/2)*(-2/3)+(5/2-3/4):7/4
=1+7/4:7/4=1+1=2
b: \(=\dfrac{1}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+...+\dfrac{3}{100\cdot103}\right)\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{103}\right)\)
=1/3*102/103=34/103
Đúng 0
Bình luận (0)
Tan2x.tanx=1 Giúp em với ạ👉👈
ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{\pi}{2}+k2\pi\)
\(tan2x.tanx=1\)
\(\Leftrightarrow\dfrac{sin2x.sinx}{cos2x.cosx}=1\)
\(\Leftrightarrow sin2x.sinx=cos2x.cosx\)
\(\Leftrightarrow\dfrac{1}{2}\left(cosx-cos3x\right)=\dfrac{1}{2}\left(cos3x+cosx\right)\)
\(\Leftrightarrow cos3x=0\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
Đúng 0
Bình luận (0)
Nhanh giúp em với ạ 👉👈💦
a: Xét ΔMEB vuông tại M và ΔACB vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔMEB\(\sim\)ΔACB
Xét ΔDMC vuông tại M và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔDMC\(\sim\)ΔABC
b: BC=30cm
Đúng 1
Bình luận (0)
👉 Không Tiền💰Không Xe 🚗 Không Sự Nghiệp ✔️👈 ! 👉 Bạn Bè 👥 Xa Lánh😞 Chẳng Ai Chơi ✔️👈 ! 👉 Không Nổi, 😵 Không Tiếng, 😰 Không Danh Vọng ✔️👈 ! 👉 Có Tình💋Có Nghĩa 👀Có Chơi Không ??? ✔👈 ! 👉 Hoa Đẹp🌸Hoa Thơm🌹Hoa Vẫn Tàn🍃 👈 ! 👉 Tình Nặng 💑Tình Sâu 👫 Tình Vẫn Tan 💔👈 ! 👉 Rượu Đắng💀Rượu Cay👽 Rượu Vẫn Hết 👌👈 ! 👉 Người Hứa ✋ Người Thề ☝ Người Vẫn Quên 💢👈 ! 👉 Trăng Lên🌝Trăng tròn 🌑Trăng Lại Khuyết 🌙👈 ! 👉 Tuyết Rơi ❄ Tuyết Phủ ⛄ Tuyết Lại Tan 💦👈 ! 👉 Hoa Nở🌺Hoa Rơi🍃...
Đọc tiếp
👉 Không Tiền💰Không Xe 🚗 Không Sự Nghiệp ✔️👈 ! 👉 Bạn Bè 👥 Xa Lánh😞 Chẳng Ai Chơi ✔️👈 ! 👉 Không Nổi, 😵 Không Tiếng, 😰 Không Danh Vọng ✔️👈 ! 👉 Có Tình💋Có Nghĩa 👀Có Chơi Không ??? ✔👈 ! 👉 Hoa Đẹp🌸Hoa Thơm🌹Hoa Vẫn Tàn🍃 👈 ! 👉 Tình Nặng 💑Tình Sâu 👫 Tình Vẫn Tan 💔👈 ! 👉 Rượu Đắng💀Rượu Cay👽 Rượu Vẫn Hết 👌👈 ! 👉 Người Hứa ✋ Người Thề ☝ Người Vẫn Quên 💢👈 ! 👉 Trăng Lên🌝Trăng tròn 🌑Trăng Lại Khuyết 🌙👈 ! 👉 Tuyết Rơi ❄ Tuyết Phủ ⛄ Tuyết Lại Tan 💦👈 ! 👉 Hoa Nở🌺Hoa Rơi🍃Hoa Lại Tàn🍂👈 ! 👉 Tình Đẹp 💏 Tình Sâu 💞 Tình Ly Tan ❣👈 ! 👉 Người Đẹp 💆 Người Xấu👹 Rồi Củng Ra Đi 👻👈 ! 👉 Người Giàu 🏣 Người Nghèo 🏠 Rồi Cũng Hết 💸👈 ! 👉Tiền Tài💰 Địa Vị 📈Cũng Sẽ Tan 💢👈 ! 👉 Cao Sang💵 Danh Vọng 👑 Cũng Sẽ Tàn 🚬👈 ! 👉 Phấn Son💄 Nhan Sắc 👰 Đâu Còn Mãi 🙀👈 ! 👉 Chỉ Có CHÂN THÀNH Sẽ Mãi Tồn Tại Với Thời Gian
Giúp e với ạ, có bài giải luôn nha 🥺👉👈
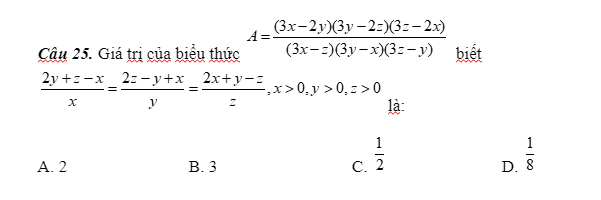
Áp dụng tc dtsbn:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\\ \Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.;\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2z\end{matrix}\right.\\ \Rightarrow P=\dfrac{xyz}{2x\cdot2y\cdot2z}=\dfrac{1}{8}\)
Chọn D
Đúng 5
Bình luận (1)
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
\(\Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.\) và \(\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2x\end{matrix}\right.\)
Thay vào A:
\(A=\dfrac{z.x.y}{2y.2z.2x}=\dfrac{1}{8}\)
Đúng 4
Bình luận (1)
Vì x>0, y>0, z>0 ⇒ x+y+z>0
Áp dụng t/c dtsbn ta có:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2y+z-x+2z-y+x+2x+y-z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
\(\dfrac{2y+z-x}{x}=2\Rightarrow2y+z-x=2x\Rightarrow2y+z=3x\\ \dfrac{2z-y+x}{y}=2\Rightarrow2z-y+x=2y\Rightarrow2z+x=3y\\ \dfrac{2x+y-z}{z}=2\Rightarrow2x+y-z=2z\Rightarrow2x+y=3z\)
\(A=\dfrac{\left(3x-2y\right)\left(3y-2z\right)\left(3z-2x\right)}{\left(3x-z\right)\left(3y-x\right)\left(3z-y\right)}\)
\(\Rightarrow A=\dfrac{\left(2y+z-2y\right)\left(2z+y-2z\right)\left(2x+y-2x\right)}{\left(2y+z-z\right)\left(2z+x-x\right)\left(2x+y-y\right)}\)
\(\Rightarrow A=\dfrac{xyz}{2x.2y.2z}\)
\(\Rightarrow A=\dfrac{1}{8}\)
Đúng 1
Bình luận (3)
Xem thêm câu trả lời
Giúp em nhanh vs ạ 👉👈💦
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
DO đó: ΔABC\(\sim\)ΔHAC
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giúp mikk với ạ 👉👈





